Em agosto de 2018 a Nasa lançou a Sonda Solar Parker, destinada a investigar o Sol, passando pela coroa solar. A sonda seguirá uma trajetória dando várias voltas em torno do Sol, em órbitas elípticas com grande excentricidade.

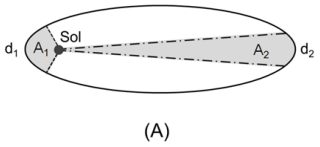
a) Considere um corpo que descreve uma órbita elíptica em torno do Sol, como ilustra a figura A. A área da elipse varrida pela linha que liga o corpo ao Sol no trecho 2 é o dobro da área varrida no trecho 1 (A2 = 2 × A1) já as distâncias percorridas nos trechos são tais que d2 = 0,8 × d1. Se a velocidade escalar média do corpo no trecho 1 é igual a v1 = 172.000 km/h , quanto vale a velocidade escalar média no trecho 2?

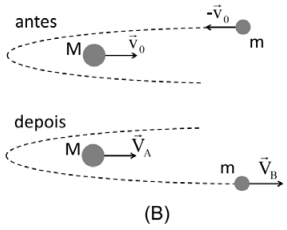
b) A sonda terá sua velocidade modificada (sem consumo adicional de combustível) nas passagens próximas ao planeta Vênus, explorando o efeito conhecido como catapulta gravitacional. Para ilustrar esse efeito, considere dois corpos de massas M e m, inicialmente com velocidades de mesmo módulo (v0), mesma direção e sentidos contrários. Após a aproximação, os corpos se afastam com velocidades de módulos VA e VB , seguindo na mesma direção inicial, conforme mostra a figura B. Como a energia cinética se conserva, a velocidade de afastamento dos corpos é igual à de aproximação: 2V0 = VB - VA Encontre a velocidade VB da massa m em termos de M, m e v0 . Em seguida, use M = 100m e encontre a razão VB/v0 .

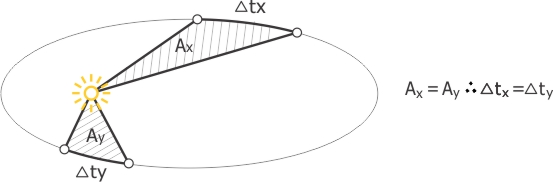
a) A 2ª lei de Kepler (lei das áreas) diz que um corpo em órbita elíptica em torno do Sol descreve áreas iguais em intervalos de tempo iguais.


começar estilo tamanho matemático 14px Como espaço reto A com 2 subscrito espaço igual a espaço 2 reto A com 1 subscrito vírgula espaço tem menos se dois pontos espaço incremento reto t com 2 subscrito espaço igual a espaço 2 espaço vezes espaço incremento reto t com 1 subscrito. Como espaço reto d com 2 subscrito espaço igual a espaço 0 vírgula 8 reto d com 1 subscrito vírgula espaço reto e espaço sendo espaço reto d espaço igual a espaço reto V espaço vezes espaço incremento reto t vírgula espaço tem menos se dois pontos reto V com 2 subscrito espaço vezes espaço incremento reto t com 2 subscrito espaço igual a espaço 0 vírgula 8 reto V com 1 subscrito espaço vezes incremento reto t com 1 subscrito reto V com 2 subscrito espaço vezes espaço riscado diagonal para cima sobre incremento reto t com 1 subscrito fim do riscado espaço igual a espaço 0 vírgula 8 espaço vezes espaço 172 espaço estreito 000 espaço vezes riscado diagonal para cima sobre incremento reto t com 1 subscrito fim do riscado então espaço reto V com 2 subscrito espaço igual a espaço 68 espaço 800 espaço tipográfico km sobre reto h em moldura de caixa fecha moldura fim do estilo​

b) Considerando o sistema (Vênus e Sonda) mecanicamente isolado, tem-se:
começar estilo tamanho matemático 14px atributos de tabela alinhamento de coluna right center left fim dos atributos linha com célula com reto Q com antes subscrito com sist sobrescrito fim da célula igual a célula com reto Q com depois subscrito com sist sobrescrito fim da célula linha com célula com reto Q com Vênus subscrito espaço mais espaço reto Q com Sonda subscrito fim da célula igual a célula com reto Q com Vênus subscrito com apóstrofo sobrescrito espaço mais reto Q espaço com Sonda subscrito com apóstrofo sobrescrito fim da célula linha com célula com MV com 0 subscrito espaço mais espaço reto m parêntese esquerdo menos reto V com 0 subscrito parêntese direito fim da célula igual a célula com MV com reto A subscrito espaço mais espaço mV com reto B subscrito fim da célula linha com célula com MV com 0 subscrito espaço menos espaço mV com 0 subscrito fim da célula igual a célula com MV com reto A subscrito espaço mais espaço mV com reto B subscrito espaço espaço espaço reto I em moldura circular fim da célula fim da tabela fim do estilo
A partir do enunciado:
começar estilo tamanho matemático 14px reto V com reto A subscrito espaço igual a espaço reto V com reto B subscrito espaço menos espaço 2 reto V com 0 subscrito espaço espaço II em moldura circular fim do estilo
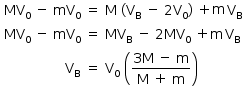
Substituindo-se começar estilo tamanho matemático 14px II em moldura circular fim do estilo em começar estilo tamanho matemático 14px reto I em moldura circular fim do estilo:


Para M = 100 · m, pode-se escrever:

começar estilo tamanho matemático 14px reto V com reto B subscrito espaço igual a espaço reto V com 0 subscrito espaço abre parênteses espaço numerador 3 espaço vezes espaço 100 espaço estreito reto m espaço menos espaço reto m sobre denominador 100 espaço estreito reto m espaço mais espaço reto m fim da fração fecha parênteses então espaço reto V com reto B subscrito sobre reto V com 0 subscrito espaço igual a espaço 299 sobre 101 espaço assimptoticamente igual espaço 2 vírgula 96em moldura de caixa fecha moldura fim do estilo