Nos cruzamentos de avenidas das grandes cidades é comum encontrarmos, além dos semáforos tradicionais de controle de tráfego de carros, semáforos de fluxo de pedestres, com cronômetros digitais que marcam o tempo para a travessia na faixa de pedestres.
a) No instante em que o semáforo de pedestres se torna verde e o cronômetro inicia a contagem regressiva, uma pessoa encontra-se a uma distância d = 20 m do ponto de início da faixa de pedestres, caminhando a uma velocidade inicial v0 = 0,5 m/s . Sabendo que ela inicia a travessia da avenida com velocidade v = 1,5 m/s , calcule a sua aceleração constante no seu deslocamento em linha reta até o início da faixa.
b) Considere agora uma pessoa que atravessa a avenida na faixa de pedestres, partindo de um lado da avenida com velocidade inicial v0 = 0,4 m/s e chegando ao outro lado com velocidade final v = 1,2 m/s. O pedestre realiza todo o percurso com aceleração constante em um intervalo de tempo de t = 15 s . Construa o gráfico da velocidade do pedestre em função do tempo e, a partir do gráfico, calcule a largura da avenida.
a) A pessoa se descola 20 m em movimento uniformemente variado (a = cte). Logo, pode-se calcular sua aceleração usando a equação de Torricelli:
b) Se a travessia da faixa de pedestres é efetuada com aceleração constante, o gráfico vxt é um segmento de reta. Admitindo-se para
, tem-se:
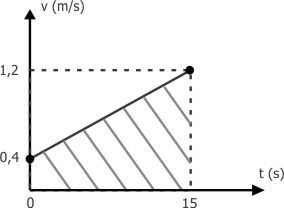
Para calcular a largura da faixa de pedestres (L) aplica-se a propriedade do gráfico vxt em que L = ΔS pode ser obtido pela área sob o gráfico.
Assim: