Os gráficos a seguir referem-se às funções exponenciais f e g, de IR em IR, definidas por f(x) = a · bx e g(x) = c + c · dx , com a, b, c e d sendo números reais, 0 < b ≠ 1 e 0 < d ≠ 1.
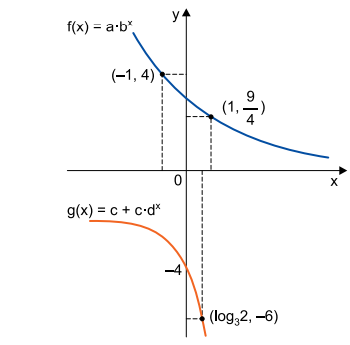
a) Determine a função f e as coordenadas do ponto de intersecção do seu gráfico com o eixo y.
b) Determine a função g e a equação da assíntota do seu gráfico.
a) Como o gráfico da função passa pelos pontos (-1, 4) e
, tem-se:
De (I) em (II), vem:
Como , tem-se que
.
Substituindo em (I):
Logo,
Além disso , portanto, o ponto de intersecção do gráfico de
com o eixo
é
.
Resp. : e
.
b) Como o gráfico da função passa pelos pontos
e
, tem-se:
De (I) em (II), vem:
Aplicando logaritmo na base 2, nos dois lados tem-se:
Assim,
O gráfico da função exponencial foi deslocado duas unidades em relação ao eixo. Assim a assíntota de
é a reta paralela ao eixo
cuja equação é dada por
Resp. : e
.