Na figura, as retas e
são paralelas, assim como as retas
e
. A distância entre e é 3 cm, mesma distância entre
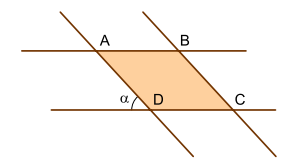
a) Calcule o perímetro do paralelogramo ABCD, formado pelas intersecções das retas, na situação em que α = 60º.
b) Considere que S seja a área do paralelogramo ABCD representado na figura. Determine S em função de α e determine a área mínima do paralelogramo ABCD.
Para responder os dois itens, leve-se em consideração as seguintes imagens e relação:
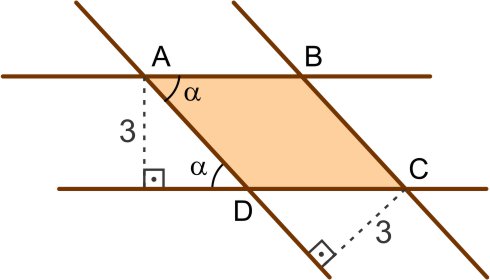
a) sendo tem-se
.
Como ABCD é um losango, o perímetro 2p, em cm, é
Repostas:
b) A área S pode ser obtida pelo dobro da área do triângulo ABD. dessa forma, a área S, em cm², é
A área S será mínima quando o denominador for máximo, isto é, em cm²
Ou seja quando ABCD for um quadrado.
Resposta: