Uma corda elástica, de densidade linear constante μ = 0,125 kg/m, tem uma de suas extremidades presa a um vibrador que oscila com frequência constante. Essa corda passa por uma polia, cujo ponto superior do sulco alinha-se horizontalmente com o vibrador, e, na outra extremidade, suspende uma esfera de massa 1,8 kg, em repouso. A configuração da oscilação da corda é mostrada pela figura 1.
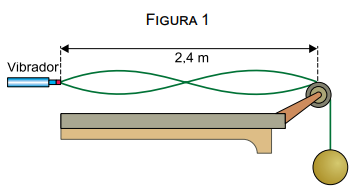
Em seguida, mantendo-se a mesma frequência de oscilação constante no vibrador, a esfera é totalmente imersa em um recipiente contendo água, e a configuração da oscilação na corda se altera, conforme figura 2.
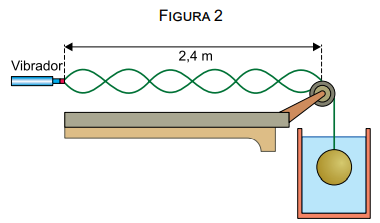
Adotando g = 10 m/s2 e sabendo que a velocidade de propagação de uma onda em uma corda de densidade linear μ, submetida a uma tração T, é dada por , calcule:
a) a frequência de oscilação, em Hz, do vibrador.
b) a intensidade do empuxo, em N, exercido pela água sobre a esfera, na situação da figura 2.
a) Na situação inicial:
I)
II) A tração (T) no fio apresenta a mesma intensidade do peso (P) do corpo:
III) A partir da equação fornecida:
IV) Na equação fundamental da ondulatória:
b) Na situação apresentada na figura 2, tem-se:
I)
II) Como e sendo
, tem-se:
III) A partir da equação fornecida
IV) As forças que atuam no corpo são:
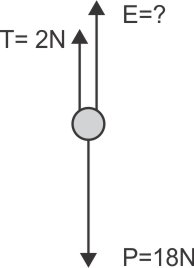
Estando o corpo em equilíbrio: