A figura representa um trapézio retângulo UNFE de altura começar estilo tamanho matemático 14px UE em moldura superior fim do estilo e uma circunferência de centro P inscrita no triângulo SNF, com S pertencente à começar estilo tamanho matemático 14px UE em moldura superior fim do estilo. Sabe-se que começar estilo tamanho matemático 14px SI em moldura superior fim do estilo é perpendicular a começar estilo tamanho matemático 14px NF em moldura superior fim do estilo, que I é o ponto médio de começar estilo tamanho matemático 14px NF em moldura superior fim do estilo e que UN = 8 cm, EF = 6 cm e ES = 8 cm.

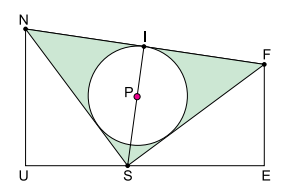
a) Calcule NS e a área do trapézio UNFE.

b) Calcule a área da região destacada em verde na figura.

Do enunciado, tem-se:

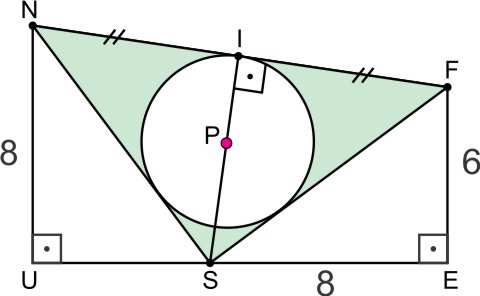
a) Pitágoras começar estilo tamanho matemático 14px parêntese esquerdo incremento espaço SEF parêntese direito fim do estilo: começar estilo tamanho matemático 14px parêntese esquerdo SF parêntese direito ao quadrado espaço igual a espaço 8 ao quadrado espaço mais espaço 6 ao quadrado espaço espaço espaço espaço espaço então espaço SF espaço igual a espaço 10 fim do estilo
Como I é ponto médio de começar estilo tamanho matemático 14px NF com barra sobrescrito espaço reto e espaço SI com barra sobrescrito fim do estilo é perpendicular a começar estilo tamanho matemático 14px NF com barra sobrescrito fim do estilo, o triângulo NFS é  isósceles (NS = FS). Portanto, começar estilo tamanho matemático 14px NS com barra sobrescrito espaço igual a espaço 10 espaço estreito cm fim do estilo 
Pitágoras começar estilo tamanho matemático 14px parêntese esquerdo incremento espaço NUS parêntese direito dois pontos espaço parêntese esquerdo US parêntese direito ao quadrado espaço mais espaço 8 ao quadrado espaço igual a espaço 10 espaço então espaço US espaço igual a espaço 6 fim do estilo
A área do trapézio UNFE é:
começar estilo tamanho matemático 14px reto A espaço igual a espaço numerador parêntese esquerdo 8 espaço mais espaço 6 parêntese direito espaço vezes espaço 14 sobre denominador 2 fim da fração espaço igual a espaço 98 fim do estilo
Resposta: NS = 10 cm; área do trapézio = começar estilo tamanho matemático 14px 98 espaço estreito cm ao quadrado fim do estilo
b) Tem-se:

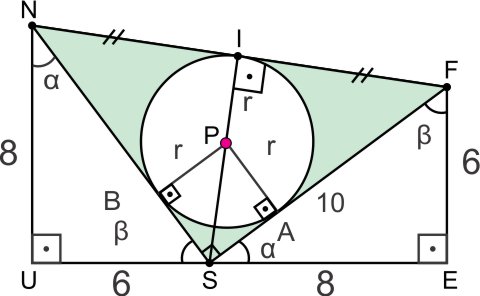
Os triângulos NUS e SEF são congruentes.
Como começar estilo tamanho matemático 14px reto alfa espaço mais espaço reto B espaço igual a espaço 90 sinal de grau fim do estilo, o ângulo de vértice S do triângulo NSF é reto.
Sendo r o raio do círculo, SAPB é um quadrado de lado r e, portanto, começar estilo tamanho matemático 14px PS espaço igual a espaço reto r raiz quadrada de 2 fim do estilo
Ainda, SFI é um triângulo retângulo isósceles. Como SF = 10, tem-se que começar estilo tamanho matemático 14px SI espaço igual a espaço 5 raiz quadrada de 2 fim do estilo.
Então:  começar estilo tamanho matemático 14px PS espaço mais espaço PI espaço igual a espaço SI reto r raiz quadrada de 2 espaço mais espaço reto r espaço igual a espaço 5 raiz quadrada de 2 espaço espaço espaço espaço espaço espaço então espaço espaço reto r espaço igual a espaço 5 espaço parêntese esquerdo 2 espaço menos espaço raiz quadrada de 2 parêntese direito fim do estilo
A área da região destacada é a diferença entre a área do triângulo e a área do círculo.
A (destacada) começar estilo tamanho matemático 14px igual a espaço 1 meio espaço vezes espaço 10 espaço vezes espaço 10 espaço menos espaço reto pi espaço abre colchetes 5 espaço parêntese esquerdo 2 espaço menos espaço raiz quadrada de 2 parêntese direito fecha colchetes ao quadrado fim do estilo,
ou seja, começar estilo tamanho matemático 14px 50 espaço menos espaço 25 reto pi espaço parêntese esquerdo 6 espaço menos espaço 4 raiz quadrada de 2 parêntese direito fim do estilo
Resposta: começar estilo tamanho matemático 14px parêntese recto esquerdo 50 espaço menos espaço 25 reto pi espaço parêntese esquerdo 6 espaço menos espaço 4 raiz quadrada de 2 parêntese direito parêntese recto direito espaço estreito cm ao quadrado fim do estilo