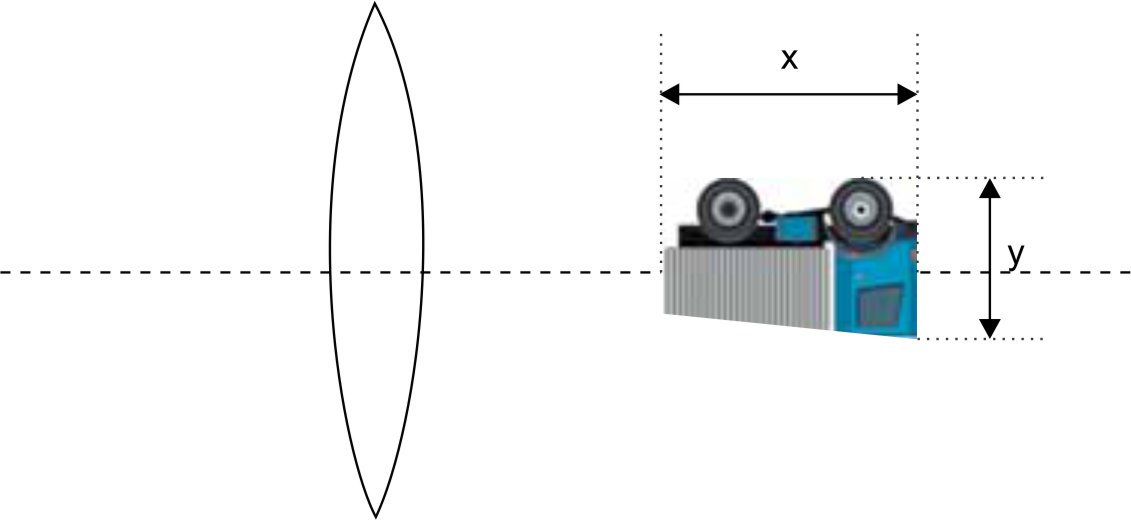
Um caminhão de 2 m de altura e 6 m de comprimento está parado a 15 m de uma lente esférica delgada de distância focal igual a 3 m. Na figura, fora de escala, estão representados o caminhão, a lente e a imagem do caminhão conjugada pela lente.
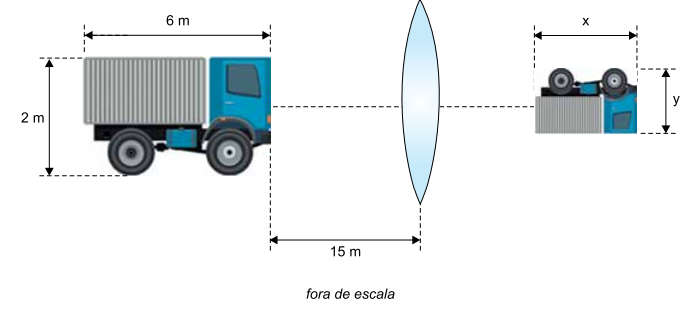
Considerando válidas as condições de nitidez de Gauss, calcule, em m:
a) a altura (y) da imagem da frente do caminhão.
b) o comprimento (x) da imagem do caminhão.
a) Considerando a frente do caminhão como um objeto linear, de comprimento 2 m, a 15 m da lente, pode-se representar a situação pelo seguinte esquema:
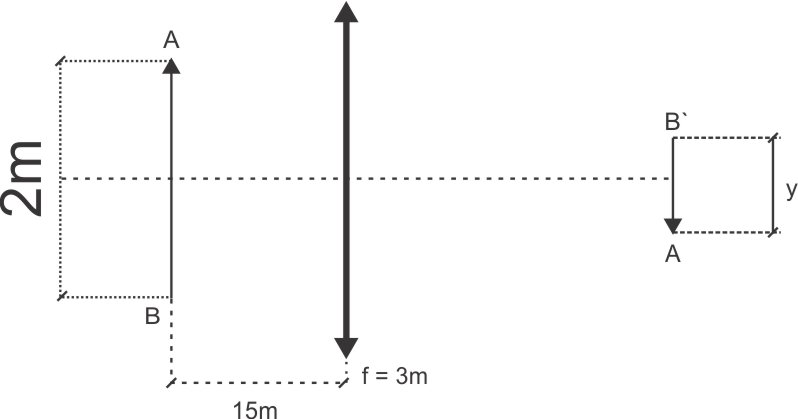
A partir da equação do aumento linear transversal:
em que: i = y; o = 2 m; f = 3 m e p = 15 m.
Assim:
Portanto, a altura da imagem da frente do caminhão vale 0,5m.
b) Aplicando a equação , para dois pontos, F e T, pertencentes, respectivamente, à frente e à traseira do caminhão, tem-se:
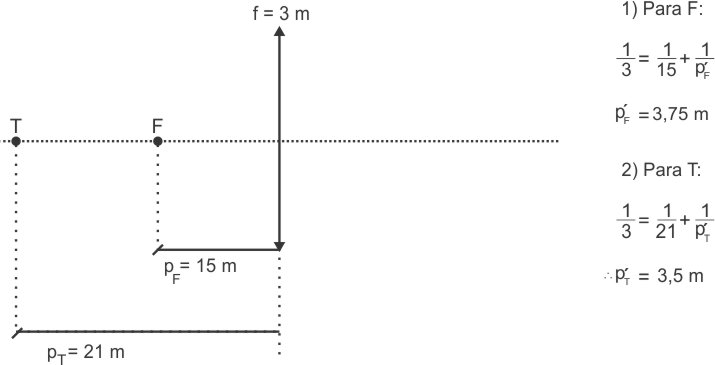
Pelos resultados
1) A imagem da frente do caminhão está a 3,75 m de distância da lente.
2) A imagem da traseira do caminhão está a 3,5 m de distância da lente.
Logo, conclui-se que o comprimento (x) da imagem do caminhão é:
Observação: Apesar de a citação da figura estar fora de escala, a imagem do caminhão, nas circunstâncias apresentadas, não corresponde àquela fornecida pelo enunciado. Na realidade, essa imagem seria mais parecida com o esquema a seguir: