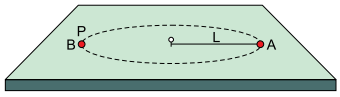
Uma esfera A desliza em movimento circular sobre uma mesa horizontal, sem atrito, presa a um pino fixo no centro da mesa por um fio ideal de comprimento L = 1 m. A energia cinética dessa esfera é constante e tem intensidade igual a 4 J. Em um ponto P é colocada, em repouso, uma segunda esfera B, idêntica à primeira, de modo que ocorra uma colisão perfeitamente inelástica entre elas, conforme indica a figura.
a) Calcule a intensidade da tração, em N, no fio antes da colisão entre as esferas.
b) Determine a energia cinética, em J, do sistema formado pelas duas esferas juntas, imediatamente após a colisão entre elas.
a) De acordo com o enunciado, .
Logo, utilizando a definição de energia cinética:
A tração no fio é a resultante centrípeta na esfera A. Logo:
Como L = 1 m e mVA2 = 8:
b) Aplicando o princípio da conservação da quantidade de movimento:
Logo, a energia cinética do sistema formado pelas duas esferas juntas é:
Como mVA2 = 8: