À medida que a parcela de ar se eleva na atmosfera, nos limites da troposfera, a temperatura do ar decai a uma razão de 1 °C a cada 100 metros (Razão Adiabática Seca ‐ RAS) ou 0,6 °C a cada 100 metros (Razão Adiabática Úmida ‐ RAU).
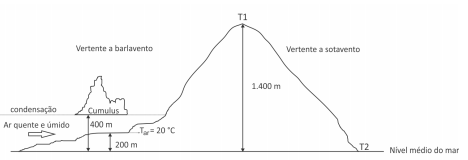
Considerando os conceitos e a ilustração, é correto afirmar que as temperaturas do ar, em graus Celsius, T1 e T2, são, respectivamente,
Note e adote:
Utilize RAS ou RAU de acordo com a presença ou não de ar saturado.
Tar: temperatura do ar.
A partir da razão adiabática seca (da superfície até a base da nuvem - Cumulus), tem-se:
Da base do Cumulus até T1, tem-se a Razão Adiática Úmida, portanto:
De T1 a T2 (Vertente a sotavento):
Portanto, a temperatura T2 é dada por: