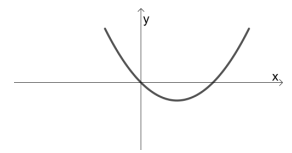
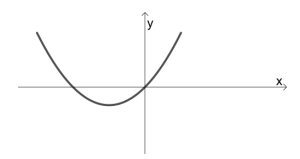
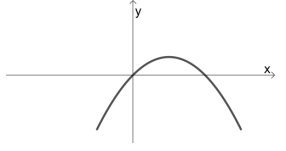
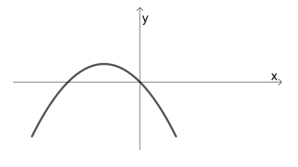
Sejam a e b números reais positivos. Considere a função quadrática f(x) = x(aa + b), definida para todo número real x. No plano cartesiano, qual figura corresponde ao gráfico de y = f(x)?

  • a

    .

  • b

  • c

  • d

Reescrevendo a lei começar estilo tamanho matemático 14px reto f parêntese esquerdo reto x parêntese direito fim do estilo, tem-se:
começar estilo tamanho matemático 14px reto f parêntese esquerdo reto x parêntese direito espaço igual a espaço reto x espaço vezes espaço parêntese esquerdo ax espaço mais espaço reto b parêntese direito reto f parêntese esquerdo reto x parêntese direito espaço igual a espaço reto a espaço vezes espaço reto x espaço vezes espaço parêntese esquerdo reto x espaço mais espaço reto b sobre reto a parêntese direito fim do estilo
Dessa forma, tem-se que suas raízes são começar estilo tamanho matemático 14px reto x com 1 subscrito espaço igual a espaço 0 fim do estilo e começar estilo tamanho matemático 14px reto x com 2 subscrito espaço igual a espaço menos reto b sobre reto a fim do estilo. Como a e b são positivos, tem-se começar estilo tamanho matemático 14px reto x com 2 subscrito espaço menor que espaço 0 fim do estilo.
Além disso, como começar estilo tamanho matemático 14px reto a espaço maior que espaço 0 fim do estilo, a parábola dada pelo gráfico de f tem concavidade voltada para cima.
A única alternativa que exibe essas características é B.