Em relação a um sistema cartesiano de eixos ortogonais com origem em O(0, 0), um avião se desloca, em linha reta, de O até o ponto P, mantendo sempre um ângulo de inclinação de 45º com a horizontal. A partir de P, o avião inicia trajetória parabólica, dada pela função f(x) = –x2 + 14x – 40, com x e f(x) em quilômetros. Ao atingir o ponto mais alto da trajetória parabólica, no ponto V, o avião passa a se deslocar com altitude constante em relação ao solo, representado na figura pelo eixo x.

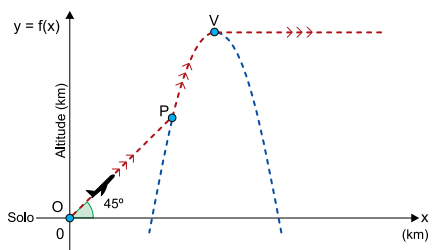
Em relação ao solo, do ponto P para o ponto V, a altitude do avião aumentou

  • a

    2,5 km. 

  • b

    3 km. 

  • c

    3,5 km. 

  • d

    4 km. 

  • e

    4,5 km.

O ponto V pertence ao gráfico da função de lei f(x) = –x2 + 14x – 40.

Sendo V = (xv, yv), tem-se:

começar estilo tamanho matemático 14px reto x com reto v subscrito espaço igual a espaço numerador menos 14 sobre denominador 2 espaço parêntese esquerdo menos 1 parêntese direito fim da fração espaço espaço espaço então espaço espaço espaço reto x com reto v subscrito espaço igual a espaço 7 reto y com reto v subscrito espaço igual a espaço reto f parêntese esquerdo 7 parêntese direito espaço espaço espaço então espaço espaço espaço reto y com reto v subscrito espaço igual a espaço 9 fim do estilo

Como P pertence à bissetriz dos quadrantes ímpares, tem-se P = (x, x).

Como P pertence ao gráfico de f, tem-se:

começar estilo tamanho matemático 14px reto f parêntese esquerdo reto x parêntese direito espaço igual a espaço reto x então espaço menos reto x ao quadrado espaço mais espaço 14 reto x espaço menos espaço 40 espaço igual a espaço reto x então espaço menos reto x ao quadrado espaço mais espaço 13 reto x espaço menos espaço 40 espaço igual a espaço 0 então espaço reto x espaço igual a espaço 5 espaço ou espaço reto x espaço igual a espaço 8. fim do estilo

Dado que a abscissa do ponto P é menor que a abscissa do vértice V, tem-se x = 5.

Assim, P = (5, 5) e V = (7, 9).

Logo, a altitude de P aumentou em 4 Km.