Ao meio-dia, a areia de um deserto recebe grande quantidade de energia vinda do Sol. Aquecida, essa areia faz com que as camadas de ar mais próximas fiquem mais quentes do que as camadas de ar mais altas. Essa variação de temperatura altera o índice de refração do ar e contribui para a ocorrência de miragens no deserto, como esquematizado na figura 1.

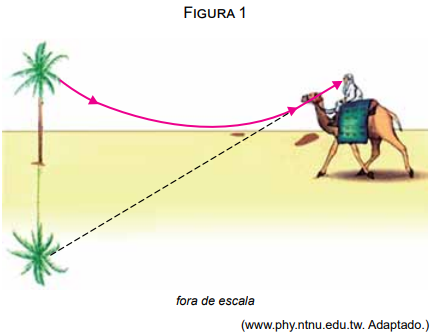
Para explicar esse fenômeno, um professor apresenta a seus alunos o esquema da figura 2, que mostra um raio de luz monocromático partindo do topo de uma palmeira, dirigindo-se para a areia e sofrendo refração rasante na interface entre as camadas de ar B e C.

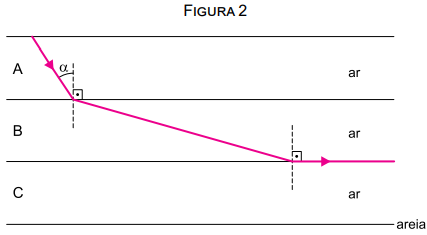
Sabendo que nesse esquema as linhas que delimitam as camadas de ar são paralelas entre si, que nA, nB e nC são os índices de refração das camadas A, B e C, e sendo α o ângulo de incidência do raio na camada B, o valor de sen α é

  • a

    começar estilo tamanho matemático 14px reto n com reto C subscrito sobre reto n com reto B subscrito fim do estilo.

  • b

    Error converting from MathML to accessible text.

  • c

    Error converting from MathML to accessible text.

  • d

    Error converting from MathML to accessible text.

  • e

    Error converting from MathML to accessible text.

Na figura 2 tem-se:

   

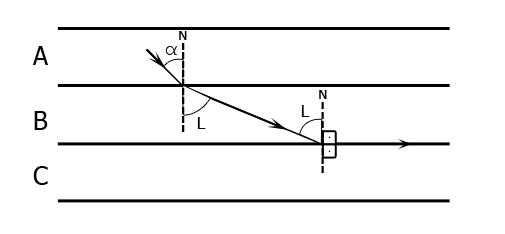
Ângulo de refração na interface AB = L

Ângulo de incidência na interface BC = L

Ângulo de refração na interface BC = 90º

Aplicando a lei de Snell – Descartes nas refrações de A para B e de B para C, tem-se:

começar estilo tamanho matemático 14px numerador sen espaço reto i sobre denominador sen espaço reto r fim da fração espaço igual a espaço reto n com passa subscrito sobre reto n com provém subscrito espaço seta dupla para a direita espaço numerador sen espaço reto alfa espaço espaço sobre denominador sen espaço reto L fim da fração espaço igual a espaço numerador começar estilo mostrar reto n com reto B subscrito fim do estilo sobre denominador reto n com reto A subscrito fim da fração espaço seta dupla para a direita reto n com reto B subscrito espaço sen espaço reto L espaço igual a espaço reto n com reto A subscrito espaço sen espaço reto alfa espaço parêntese esquerdo reto I parêntese direito espaço fim do estilo

numerador s e n espaço i sobre denominador s e n espaço r fim da fração espaço igual a espaço numerador começar estilo mostrar n com p a s s a subscrito fim do subscrito fim do estilo sobre denominador n com p r o v é m subscrito fim do subscrito fim da fração seta dupla para a direita numerador s e n espaço L sobre denominador s e n espaço 90 sinal de grau fim da fração espaço igual a espaço numerador começar estilo mostrar n com C subscrito fim do estilo sobre denominador n com B subscrito fim da fração seta dupla para a direita n com B subscrito espaço s e n espaço L espaço igual a espaço n com C subscrito espaço vezes espaço 1 espaço parêntese esquerdo I I parêntese direito

Assim, a partir das equações (I) e (II) tem-se:

n com A subscrito espaço s e n espaço alfa espaço igual a espaço n com C subscrito espaço espaço então espaço espaço s e n espaço alfa espaço igual a espaço n com C subscrito sobre n com A subscrito