Duas caixas, A e B, estão apoiadas, em repouso, sobre uma barra homogênea reta presa pelo seu ponto médio (ponto O) ao teto por meio de um fio inextensível. A caixa A está colocada a uma distância x do ponto O e a caixa B a uma distância y desse ponto. Nessa situação, a barra exerce sobre a caixa A uma força e, sobre a caixa B, uma força
.
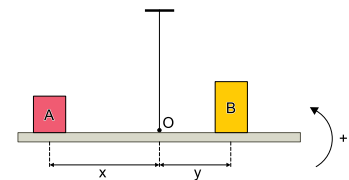
Uma matriz quadrada M é construída de forma que seus elementos são as intensidades de e
e as distâncias x e y, tal que
. Sendo Mt a matriz transposta de M e considerando-se o sentido anti-horário como o positivo para a rotação, para que a barra permaneça em equilíbrio na horizontal é necessário que
A figura a seguir ilustra as forças aplicadas na barra:
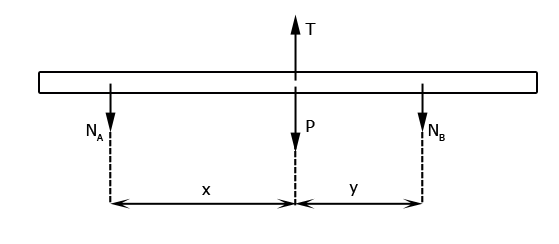
Como a barra está em equilíbrio:
ΣM0 = 0 ![]()
NA · x + T · 0 + P · 0 - NB · y = 0
NA · x - NB · y = 0
Calculando-se o determinante da matriz M:
detM = NA · x - NB · y
Assim, detM = 0
Como detMt = detM,