Para decorar um cilindro circular reto será usada uma faixa retangular de papel transparente, na qual está desenhada em negrito uma diagonal que forma 30° com a borda inferior. O raio da base do cilindro mede cm, e ao n enrolar a faixa obtém-se uma linha em formato de hélice, como na figura.
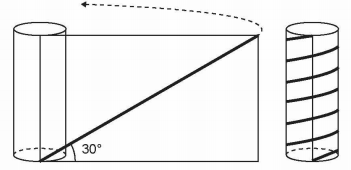
O valor da medida da altura do cilindro, em centímetro, é
- a
36
- b
24
- c
4
- d
36
- e
72
O comprimento C da circunferência da base do cilindro é tal que:
De acordo com a figura dada no enunciado, a faixa de papel dá 6 voltas completas no cilindro ao ser enrolada. Assim, o comprimento da faixa é , ou seja, 72 cm.
Então, tem-se a figura, em que h é a medida da altura do cilindro, em centímetros:
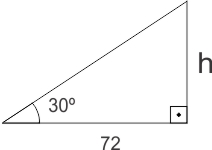
Portanto, a altura do cilindro mede