A figura mostra uma praça circular que contém um chafariz em seu centro e, em seu entorno, um passeio. Os círculos que definem a praça e o chafariz são concêntricos.

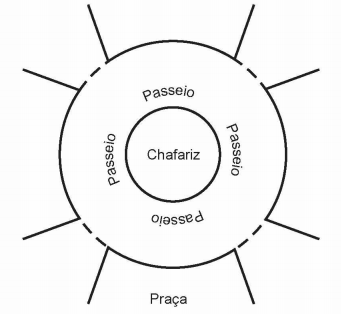
O passeio terá seu piso revestido com ladrilhos. Sem condições de calcular os raios, pois o chafariz está cheio, um engenheiro fez a seguinte medição: esticou uma trena tangente ao chafariz, medindo a distância entre dois pontos A e B, conforme a figura. Com isso, obteve a medida do segmento de reta AB: 16 m.

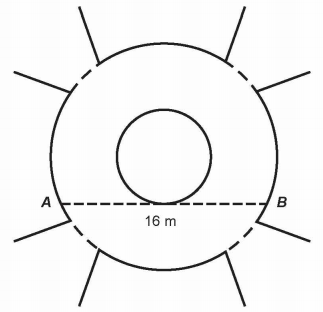
Dispondo apenas dessa medida, o engenheiro calculou corretamente a medida da área do passeio, em metro quadrado.

A medida encontrada pelo engenheiro foi

  • a

    4π.

  • b

    8π

  • c

    48π

  • d

    64π

  • e

    192π

Sendo r e R as medidas dos raios das circunferências que delimitam o Passeio, com R > r, tem-se a figura:

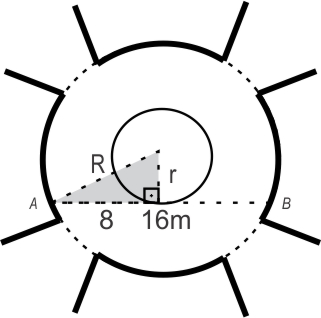
Aplicando o teorema de Pitágoras no triângulo retângulo destacado, tem-se R à potência de 2 espaço fim do exponencial igual a espaço r ao quadrado espaço mais espaço 8 ao quadrado espaço e vírgula espaço espaço p o r tan t o vírgula espaço R à potência de 2 espaço fim do exponencial menos espaço r ao quadrado espaço igual a espaço 64 espaço parêntese esquerdo I parêntese direito.
A área pedida pode ser obtida pela diferença entre a área do círculo cujo raio mede R e a do círculo cujo raio mede r e é dada por pi espaço. espaço R ao quadrado espaço menos espaço pi espaço. espaço r ao quadrado vírgula espaço o u espaço s e j a vírgula espaço pi espaço. espaço parêntese esquerdo R ao quadrado espaço menos espaço r ao quadrado parêntese direito espaço parêntese esquerdo I I parêntese direito.
De (I) e (II), tem-se que esta área, em metro quadrado, vale começar estilo tamanho matemático 14px 64 reto pi. fim do estilo