Em desenhos animados é comum vermos a personagem tentando impulsionar um barco soprando ar contra a vela para compensar a falta de vento. Algumas vezes usam o próprio fôlego, foles ou ventiladores. Estudantes de um laboratório didático resolveram investigar essa possibilidade. Para isso, usaram dois pequenos carros de plástico, A e B, instalaram sobre estes pequenas ventoinhas e fixaram verticalmente uma cartolina de curvatura parabólica para desempenhar uma função análoga á vela de um barco. No carro B inverteu-se o sentido da ventoinha e manteve-se a vela, a fim de manter as características físicas do barco, massa e formato da cartolina. As figuras representam os carros produzidos. A montagem do carro A busca simular a situação dos desenhos animados, pois a ventoinha está direcionada para a vela.

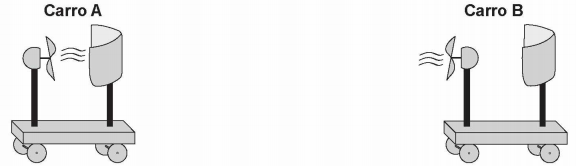
Com os carros orientados de acordo com as figuras, os estudantes ligaram as ventoinhas, aguardaram o fluxo de ar ficar permanente e determinaram os módulos das velocidades médias dos carros A (VA) e B (VB) para o mesmo intervalo de tempo.

A respeito das intensidades das velocidades médias e do sentido de movimento do carro A, os estudantes observaram que:

  • a

    VA = 0; VB > 0; o carro A não se move.

  • b

    0 < VA < VB; o carro A se move para a direita.

  • c

    0 < VA < VB; o carro A se move para a esquerda.

  • d

    0 < VB < VA; o carro A se move para a direita.

  • e

    0 < VB < VA; o carro A se move para a esquerda.

Carro A
Vamos analisar o movimento do carro A:

1) Entre o instante que o ventilador é ligado e o instante que o ar atinge a vela
O ventilador empurra o ar para à direita. Logo, de acordo com o princípio da ação e reação, o ar aplica força no ventilador para a esquerda.
Na direção horizontal essa é a única força aplicada no carro A, que inicia movimento para a esquerda.

2) Após o instante que o ar atinge a vela
A força aplicada pelo ar no ventilador não muda e podemos obter a intensidade por meio do teorema do impulso

começar estilo tamanho matemático 14px pilha reto I com reto R subscrito com seta para a direita acima espaço igual a espaço pilha incremento reto Q com seta para a direita acima espaço seta dupla para a direita pilha reto F com reto m subscrito com seta para a direita acima espaço vezes espaço incremento reto t espaço igual a espaço reto m espaço vezes pilha incremento reto V com seta para a direita acima então reto F com seta para a direita sobrescrito espaço igual a espaço numerador reto m sobre denominador incremento reto t espaço fim da fração espaço pilha incremento reto V com seta para a direita acima fim do estilo

Sendo o quociente começar estilo tamanho matemático 14px tipográfico numerador reto m sobre denominador incremento reto t fim da fração fim do estilo a razão começar estilo tamanho matemático 14px parêntese esquerdo reto Z parêntese direito fim do estilo em massa

começar estilo tamanho matemático 14px reto F com seta para a direita sobrescrito espaço igual a espaço reto Z espaço pilha incremento reto V com seta para a direita acima fim do estilo

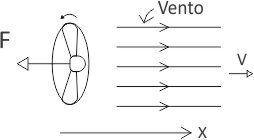
Representando o ventilador esquematicamente podemos assim obter o módulo da força começar estilo tamanho matemático 14px reto F com seta para a direita sobrescrito fim do estilo

 

começar estilo tamanho matemático 14px reto F espaço igual a espaço reto Z espaço incremento reto V com reto x subscrito espaço igual a espaço reto Z espaço vezes espaço parêntese esquerdo reto V espaço menos espaço 0 parêntese direito então espaço linha vertical reto F linha vertical espaço igual a espaço reto Z espaço reto V espaço espaço espaço espaço espaço parêntese esquerdo 1 parêntese direito fim do estilo

O ar chegando à vela pode assim ser representado

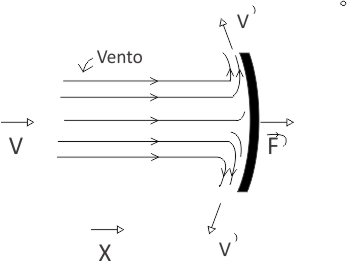
Quando o ar atinge a vela, ele aplica uma força começar estilo tamanho matemático 14px parêntese esquerdo reto F com seta para a direita sobrescrito parêntese direito fim do estilo na vela, cujo módulo pode ser obtido por meio do teorema do impulso

 

começar estilo tamanho matemático 14px linha vertical reto F apóstrofo linha vertical espaço igual a espaço reto Z espaço linha vertical incremento reto V apóstrofo com reto x subscrito linha vertical então linha vertical reto F apóstrofo linha vertical espaço igual a espaço reto Z espaço parêntese esquerdo reto V apóstrofo com reto x subscrito espaço mais espaço estreito reto V parêntese direito espaço espaço espaço espaço parêntese esquerdo 2 parêntese direito fim do estilo

Comparando as expressões (1) e (2) e admitindo a mesma vazão em massa, sendo começar estilo tamanho matemático 14px reto V apóstrofo com reto x subscrito fim do estilo diferente de zero, vemos que começar estilo tamanho matemático 14px linha vertical reto F apóstrofo linha vertical espaço maior que espaço linha vertical reto F linha vertical fim do estilo, o que nos permite afirmar que a resultante e aceleração são para a direita. A resultante pode assim ser obtida:

começar estilo tamanho matemático 14px reto R com reto A subscrito espaço igual a espaço reto F apóstrofo espaço menos espaço reto F espaço igual a espaço ZV com reto x subscrito espaço mais espaço estreito ZV espaço igual a espaço ZV então espaço reto R com reto A subscrito espaço igual a espaço ZV com reto x subscrito espaço espaço espaço espaço parêntese esquerdo 3 parêntese direito fim do estilo

Como a aceleração é para a direita, vemos que o carro A em certo instante para, inverte o sentido do movimento, se movimentando para a direita.

Carro B
Representando esquematicamente o ventilador no carro B

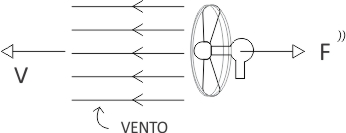
O ventilador aplica força no ar para a esquerda, logo, o ar vai aplicar força começar estilo tamanho matemático 14px parêntese esquerdo reto F com seta para a direita sobrescrito " parêntese direito fim do estilo no ventilador para a direita, cujo módulo pode assim ser obtido

começar estilo tamanho matemático 14px linha vertical reto F " linha vertical espaço igual a espaço reto Z linha vertical incremento reto V com reto x subscrito linha vertical então espaço linha vertical reto F " linha vertical espaço igual a espaço ZV espaço espaço espaço espaço espaço espaço espaço espaço parêntese esquerdo 4 parêntese direito fim do estilo

Comparando-se (3) e (4), como começar estilo tamanho matemático 14px reto V espaço maior que espaço reto V com reto x subscrito fim do estilo, concluímos que a velocidade que o carro B desenvolve começar estilo tamanho matemático 14px parêntese esquerdo reto V com reto B subscrito parêntese direito fim do estilo é maior que a velocidade que o carro A desenvolve começar estilo tamanho matemático 14px parêntese esquerdo reto V com reto A subscrito parêntese direito fim do estilo.