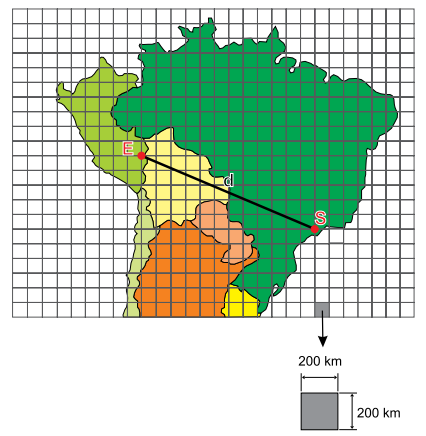
Apoiado em uma malha quadriculada, o mapa apresenta a posição do epicentro de um sismo, indicado por S, e a posição de uma estação de medição, indicada por E.
A magnitude (M) de um sismo, na escala Richter, é obtida a partir da análise de um sismograma e da distância (d), em km, entre o epicentro do sismo e a estação onde foi realizada a medição.
Para o caso indicado no mapa, considere que a relação entre a magnitude do sismo e a distância entre a estação e o epicentro seja descrita por:
M = M(d) = –5,02 + 2,8 ⋅ logd
Usando log2 = 0,3 e log13 = 1,1 a magnitude desse sismo foi igual a
Alternativa A
Na malha quadriculada, a distância d é dada pela medida da hipotenusa de um triângulo retângulo cujos catetos medem 5 unidades e 12 unidades.
Assim,
d2 = 52 = + 122 d = 13
Como cada unidade da malha representa 200 km tem-se:
M = - 5,02 + 2,8 . log (13 . 200)
M = - 5,02 + 2,8 . (log 13 + log 2 + log 100)
M = - 5,02 + 2,8 . (1,1 + 0,3 + 2)
M = - 5,02 + 9,52
M = 4,5
Logo, a magnitude dessa sismo foi igual a 4,5.