Um tubo cilíndrico está totalmente cheio de água e tem uma torneira fechada em sua parte inferior. Quando a torneira é aberta, a água escoa, fazendo com que seu nível, dentro do cilindro, abaixe com uma velocidade constante de 1 cm/s. Um diapasão de frequência 440 Hz é colocado para vibrar próximo à extremidade superior do cilindro e a torneira é aberta.
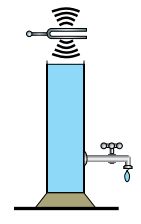
Sabendo que a velocidade de propagação do som no ar dentro do tubo cilíndrico é 352 m/s, o intervalo de tempo necessário para que sejam produzidas, dentro desse tubo, ondas sonoras estacionárias com frequência igual à do modo fundamental de ressonância é de
Alternativa C
O modo fundamental corresponde ao 1° harmônico no tubo (fechado em uma das extremidades).
A figura a seguis ilustra a configuração da onda estacionária no interior do tubo nesta situação

Na equação fundamental da ondulatória:
Como a água escoa na taxa de 1 cm/s, a posição do seu nível atingirá 20 cm após 20s.