Um adulto brinca com uma criança segurando-a pelos braços, fazendo-a girar de modo que seu centro de massa (CM) descreve um movimento circular e uniforme em uma circunferência de centro C e raio R = 2 m contida em um plano horizontal. Os braços do adulto e os da criança estão alinhados em uma direção que faz com a vertical um ângulo θ, tal que sen θ = 0,780 e cos θ = 0,624.
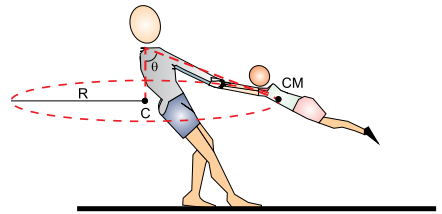
Adotando g = 10 m/s2 e desprezando a resistência do ar, a velocidade angular com a qual a criança está rodando é
Alternativa A
As forças aplicadas ao centro de massa da criança estão representadas a seguir:
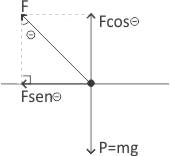
- F é a força que o adulto aplica na criança
- P é o peso da criança
1) Na direção vertical, a resultante é nula:
2) Na direção horizontal, há a resultante centrípeta.
Dividindo a equação II pela equação I:
Fazendo as devidas substituições numéricas: