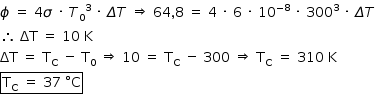Termômetros clínicos convencionais, de uso doméstico, normalmente baseiam-se na expansão térmica de uma coluna de mercúrio ou de álcool, ao qual se adiciona um corante. Com a expansão, o líquido ocupa uma parte maior de uma coluna graduada, na qual se lê a temperatura.
a) O volume de álcool em um termômetro é V0 = 20 mm3 a 25 °C, e corresponde à figura (a). Quando colocado em contato com água aquecida, o termômetro apresenta a leitura mostrada na figura (b). A escala está em milímetros, a área da secção reta da coluna é A = 5,0 x 10-2 mm2 . O aumento do volume, ∆V, produzido pelo acréscimo de temperatura ∆T, é dado por ΔT. Se para o álcool γ = 1,25 x 10-3 °C-1 , qual é a temperatura T da água aquecida?
b) Os termômetros de infravermelho realizam a medida da temperatura em poucos segundos, facilitando seu uso em crianças. Seu funcionamento baseia-se na coleta da radiação infravermelha emitida por parte do corpo do paciente. A potência líquida radiada por unidade de área do corpo humano é dada por a constante de Stefan-Boltzmann, T0 = 300 K a temperatura ambiente e ∆T = Tcorpo – T0 a diferença entre a temperatura do corpo, que deve ser medida, e a temperatura ambiente. Sabendo que em certa medida de temperatura Φ = 64,8 W/m2 , encontre a temperatura do paciente em °C. Lembre-se que θ (°C) ~ T (K) - 273.
a) Da leitura da escala, a variação do comprimento da escala é de 13 mm. Assim, a variação do volume é dada por:
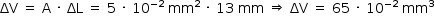
De acordo com a expressão fornecida no enunciado:
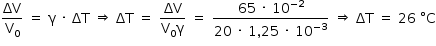
Portanto, a temperatura final será:
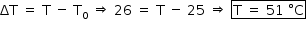
b) Substituindo os valores fornecidos na expressão dada, tem-se: