Importantes estudos sobre o atrito foram feitos por Leonardo da Vinci (1452-1519) e por Guillaume Amontons (1663-1705). A figura (a) é uma ilustração feita por Leonardo da Vinci do estudo sobre a influência da área de contato na força de atrito.
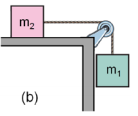
a) Dois blocos de massas m1 = 1,0 kg e m2 = 0,5 kg são ligados por uma corda e dispostos como mostra a figura (b). A polia e a corda têm massas desprezíveis, e o atrito nas polias também deve ser desconsiderado. O coeficiente de atrito cinético entre o bloco de massa m2 e a superfície da mesa é μc = 0,8. Qual deve ser a distância de deslocamento do conjunto para que os blocos, que partiram do repouso, atinjam a velocidade v = 2,0 m/s?
b) Em certos casos, a lei de Amontons da proporcionalidade entre a força de atrito cinético e a força normal continua válida nas escalas micrométrica e nanométrica. A figura (c) mostra um gráfico do módulo da força de atrito cinético, Fat, em função do módulo da força normal, N, entre duas monocamadas moleculares de certa substância, depositadas em substratos de vidro. Considerando N = 5,0 nN, qual será o módulo do trabalho da força de atrito se uma das monocamadas se deslocar de uma distância d = 2,0 μm sobre a outra que se mantém fixa?
a) O esquema seguinte mostra as forças aplicadas nos blocos 1 e 2:
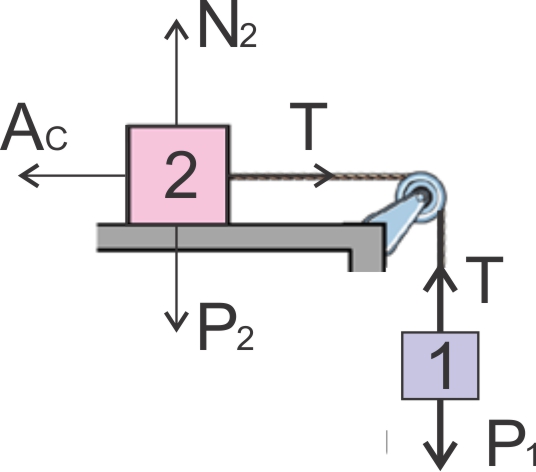
Sendo:

Aplicando a 2ª Lei de Newton para os blocos 1 e 2:
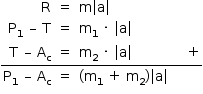
Substituindo-se os valores numéricos:
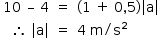
Aplicando-se a equação de Torricelli:
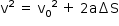
Logo, para atingir a velocidade de 2 m/s a partir do repouso:
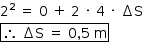
b)
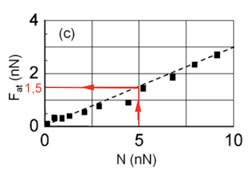
Utilizando-se o gráfico fornecido pelo enunciado, tem-se que, para 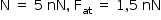 .
.
Portanto, o trabalho da força de atrito pode ser calculado como segue:
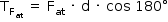
Substituindo-se os valores numéricos: