Um gigantesco iceberg desprendeu-se recentemente da Antártida, no extremo sul do planeta. O desprendimento desse iceberg, batizado de A68, foi considerado um dos maiores eventos do gênero já registrados pela ciência moderna. Segundo a NASA, é difícil prever se o iceberg permanecerá como um único bloco, mas é mais provável que ele se fragmente.
a) Considere que o iceberg tem o formato aproximado de uma placa de 6000 km2 de área e 500 m de espessura. Sendo a densidade do gelo ρg = 900 kg/m3 , calcule o empuxo sobre o iceberg que o mantém flutuando.
b) Suponha um iceberg com velocidade de deriva constante. Em um dado momento, tensões internas fazem com que dois blocos de gelo menores, A e B, se desprendam e sejam lançados em sentidos opostos e perpendicularmente à direção da velocidade de deriva do iceberg. As massas dos blocos são mA = 2,0 x 105 kg e mB = 5,0 x 104 kg. Sabendo que imediatamente após a fragmentação a direção da velocidade de deriva do iceberg se mantém, e que o módulo da velocidade do bloco A é vA = 0,5 m/s, calcule o módulo da velocidade do bloco B imediatamente após a ruptura.
a) Como o iceberg flutua em equilíbrio:

b) As figuras seguintes mostram o iceberg, em vista superior, antes e depois da sua fragmentação:
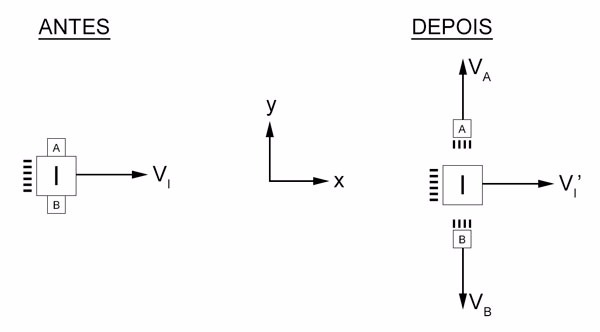
Considerando-se o sistema isolado na direção y:
