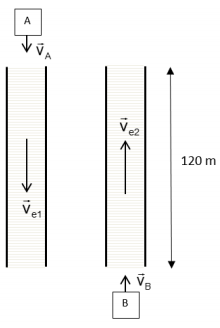
Esteiras rolantes horizontais são frequentemente instaladas em grandes aeroportos para facilitar o deslocamento das pessoas em longos corredores. A figura ao lado mostra duas esteiras rolantes que se deslocam em sentidos opostos com velocidades constantes em relação ao piso em repouso e de mesmo módulo, igual a 1,0 m/s. Em um mesmo instante, duas pessoas (representadas por A e B) que se deslocavam com velocidade constante de módulo igual a vA = 1,5 m/s e vB = 0,5 m/s em relação ao piso e em sentidos contrários entram nas esteiras e continuam caminhando como anteriormente, como mostra a figura. As esteiras rolantes têm comprimento total de 120 m.
a) Calcule o tempo necessário para que a pessoa A chegue até a outra extremidade da esteira rolante.
b) Quanto tempo depois de entrarem nas esteiras as pessoas A e B passam uma pela outra?
a) Quando A começa a andar na esteira, tem-se:
Como A se movimenta no mesmo sentido da esteira 1:
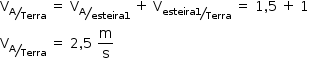
Já que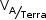 
é constante, é igual à Vm:
b) Como B se movimenta no mesmo sentido da esteira 2, e considerando 
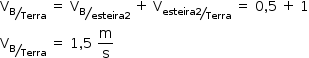
Para determinar o instante em que as pessoas A e B passam uma pela outra, é possível usar um tratamento escalar:
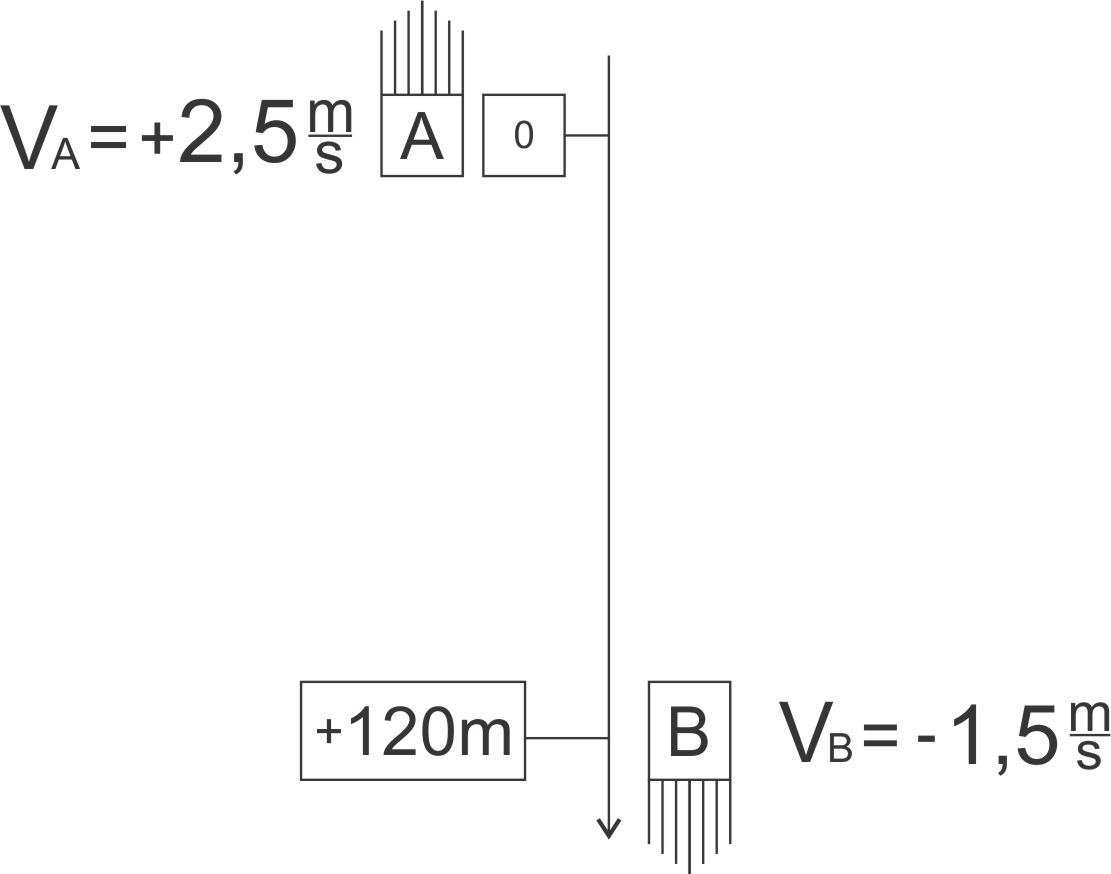
Como A e B realizam MU:
