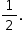Sabendo que p e q são números reais, considere as matrizes
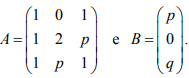
a) Prove que para quaisquer p e q teremos BTAB ≥ 0.
b) Determine os valores de p e q para os quais o sistema linear nas variáveis reais x, y e z,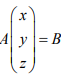 
, tem infinitas soluções.
a) Efetuando o produto, tem-se:
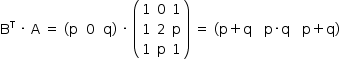
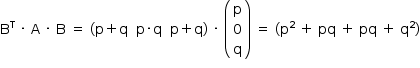
Assim, o único elemento da matriz BT · A · B é dado por p2 + 2 pq + q2, ou seja, (p + q)2. Note-se que (p + q)2 ≥ 0, para quaisquer valores reais de p e q.
b) Uma condição necessária para que o sistema seja possível e indeterminado é
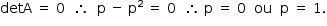
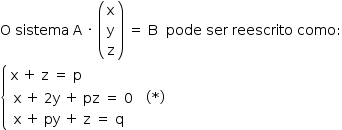
- Se p = 0, substituindo em (*), tem-se
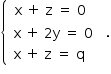Note-se que, nesse caso, o sistema será S.P.I. se, e somente se, q = 0. - Se p = 1, substituindo em (*), tem-se
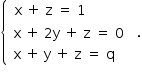Somando as duas primeiras equações do sistema, tem-se 2x + 2y + 2z = 1, ou seja, 
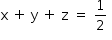. Assim, o sistema será S.P.I. se, e somente se, 
.
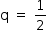Resposta: p = 0 e q = 0 ou p = 1 e q = 