A figura abaixo exibe um triângulo com lados de comprimentos a, b e c e ângulos internos θ, 2θ e β.
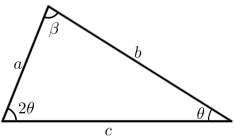
a) Supondo que o triângulo seja isósceles, determine todos os valores possíveis para o ângulo θ.
b) Prove que, se c = 2α, então β = 90°.
a) Se o triângulo é isósceles:
Resposta: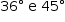 
b) Traçando-se a bissetriz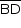 
do ângulo de vértice B e 
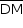perpendicular a 
.
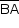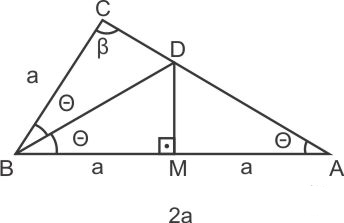
O triângulo BAD é isósceles. Então:
BM = MA = a
Os triângulos BMD e BCD são congruentes pois:
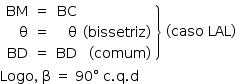
Outro modo:
