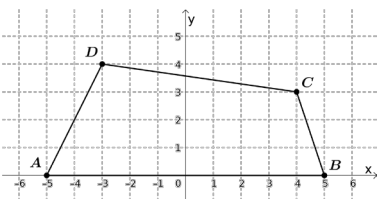
A figura abaixo exibe, no plano cartesiano, um quadrilátero com vértices situados nos pontos de coordenadas A = (−5,0), B = (5,0), C = (4,3) e D = (−3,4).
a) Determine a área desse quadrilátero.
b) Encontre a equação da reta que passa pelo ponto A e é perpendicular à reta que passa pelos pontos B e C.
a) Sendo P (–3, 0) e Q (4,0), a área S do quadrilátero ABCD é dada pela soma das áreas dos triângulos ADP e BCQ e do trapézio CDPQ. Assim, tem-se:
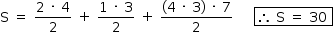
b) O coeficiente angular da reta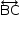 
vale 
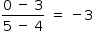; portanto, o coeficiente angular de uma reta perpendicular à 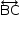vale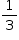 
.
A reta que passa por A (–5, 0) e é perpendicular a 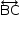tem equação
