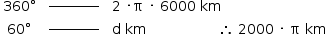Para responder aos itens a) e b), considere a figura correspondente.
a) Num tetraedro OABC, os ângulos AÔS, BÔC e CÔA medem 90°. Sendo α e β as medidas dos ângulos e
, respectivamente, expresse o cosseno do ângulo
em função de α e β.
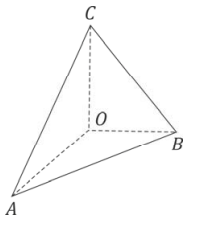
b) Um navio parte do ponto de latitude 0° e longitude 0° e navega até chegar a um ponto de latitude 45° sul e longitude 45° oeste, seguindo a trajetória que minimiza a distância percorrida. Admita que a Terra seja esférica de raio R = 6000 km. Qual foi a distância percorrida pelo navio?
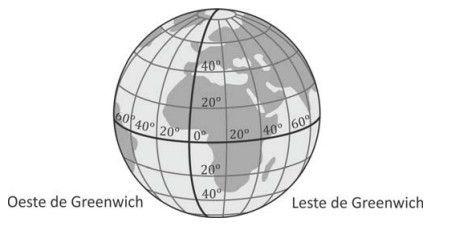
a)
Da figura, tem-se:
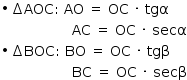
Aplicando o teorema de Pitágoras no triângulo AOB e o teorema dos cossenos no triângulo ACB, tem-se a igualdade:
b)
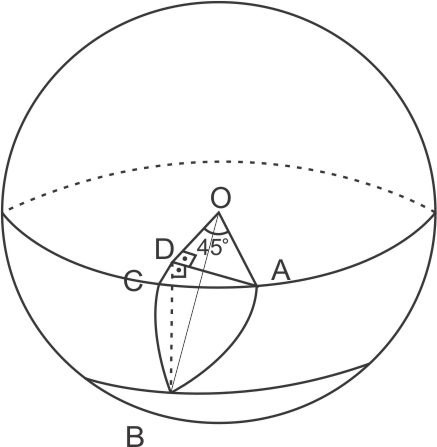
Considere-se a figura acima, que contém os pontos na superfície terrestre, A e B, com coordenadas geográficas A (0,0) e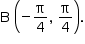 
Da figura, tem-se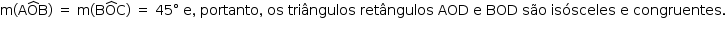 
O triângulo retângulo ADB também é isósceles, com catetos com medidas iguais às dos catetos do triângulo BOD; logo, o triângulo ADB é congruente aos triângulos BOD e AOD, portanto, AB = OA = OB.
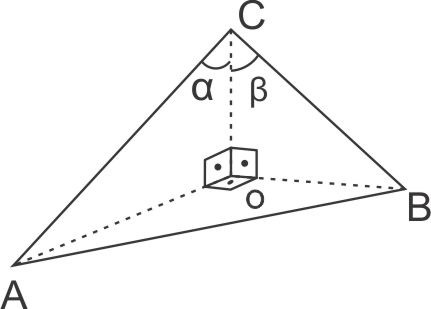
Assim, o triângulo ABO é equilátero e, dessa forma, a medida do ângulo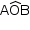 
é 60°. Sendo d o comprimento do arco 
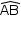(a distância pedida), tem-se:
