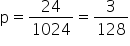Em uma competição de vôlei, estão inscritos 5 times. Pelo regulamento, todos os times devem se enfrentar apenas uma vez e, ao final da competição, eles serão classificados pelo número de vitórias. Dois ou mais times com o mesmo número de vitórias terão a mesma classificação. Em cada jogo, os times têm probabilidade de vencer.
a) Explique por que 2 times não podem empatar na classificação com 4 vitórias cada um.
b) Qual é a probabilidade de que o primeiro classificado termine a competição com 4 vitórias?
c) Qual é a probabilidade de que os 5 times terminem empatados na classificação?
a) Como cada time joga 4 partidas. Se um deles tiver 4 vitórias, significa que derrotou todos os demais, logo, nenhum outro time poderá ter 4 vitórias, pois teria sofrido pelo menos uma derrota.
b) A probabilidade de um dos 5 times vencer as 4 partidas é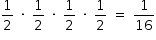 
.
Como não é possível que dois times vençam as quatro partidas (item a), tem-se que a probabilidade pedida é 
.
c)
Como cada time joga exatamente 4 vezes, a única maneira de haver empate na pontuação entre todos os times é quando cada um deles ganha 2 jogos e perde 2 jogos.
Sejam A, B, C, D e E os 5 times.
Vamos fixar uma configuração para o time A (vitória sobre os times B e C e derrota para os times D e E) e ver as possibilidades para os demais times.
Nas tabelas a seguir V e D significam, respectivamente, vitória e derrota do time da linha sobre o time da coluna da posição na qual a letra (V ou D) se encontra.
1º Caso
Time B ganha dos times C e D, e perde do time E
Neste caso, há apenas uma maneira de se completar a tabela.
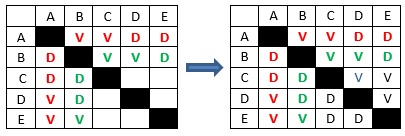
2º Caso
Time B ganha dos times C e E, e perde do time D
Neste caso, também há apenas uma maneira de se completar a tabela.
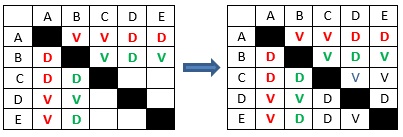
3º Caso
Time B ganha dos times D e E, e perde do time C
Neste caso, há duas maneiras de se completar a tabela.
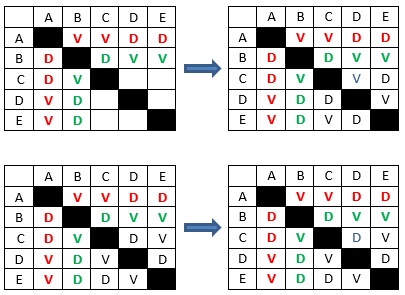
Assim, para cada configuração do time A, há exatamente 4 maneiras de se completar a tabela.
Como há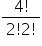 
maneiras de se configurar as duas vitórias e duas derrotas do time A, então há 
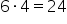maneiras de todos os times terminarem empatados.
Como há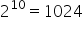 
maneiras de se determinar todos os possíveis resultados de todos os jogos desses cinco times entre si, logo a probabilidade pedida é:
