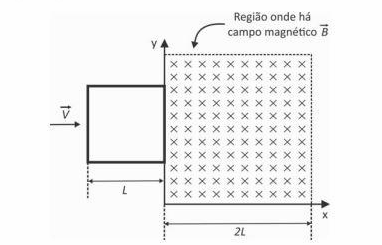
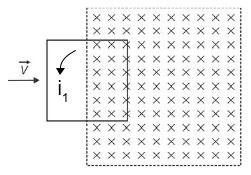
Uma espira quadrada, de lado L, constituída por barras rígidas de material condutor, de resistência elétrica total R, se desloca no plano xy com velocidade constante, na direção do eixo x. No instante t = 0, representado na figura, a espira começa a entrar em uma região do espaço, de seção reta quadrada, de lado 2L, onde há um campo magnético
perpendicular a
velocidade da espira é mantida constante por meio da ação de um agente externo. O campo
é uniforme, constante e tem a direção do eixo z, entrando no plano xy.
a) A figura da página de respostas representa a situação para o instante t1 = L/(2v). Indique nessa figura o sentido da corrente elétrica i2 que circula pela espira e determine o seu valor.
b) Determine a corrente i2 na espira para o instante t2 = (3L)/(2v).
c) Determine a força eletromagnética (módulo, direção e sentido) que atua na espira no instante t3 = (5L)/(2v).
Note e adote:
Força eletromotriz na espira parcialmente imersa no campo magnético: = L B v
a) Como a velocidade 
é constante, pode-se, assim, calcular o quanto a espira desloca-se na região de campo magnético uniforme 
até o instante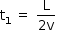 
:
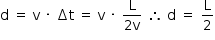
Analisando a situação descrita no enunciado entre os instantes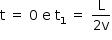 
:
- A expira entra (em parte) na região na qual há campo magnético, logo, o fluxo eletromagnético
que atravessa a espira aumenta. - Como o fluxo 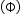aumenta, há um campo magnético induzido
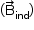na mesma direção e sentido oposto ao campo original 
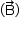dado. - Sabendo que o campo induzido 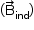é na direção z e saindo do plano xy e utlizando a regra da mão direita, conclui-se que a corrente elétrica induzida (i1) na espira é no sentido anti-horário.
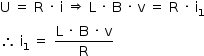
Como no instante 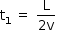a espira está parcialmente imersa no campo magnético, pode-se assim calcular a corrente elétrica (i1):
b) Calculando a posição da espira no instante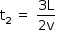 
:
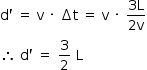
Nesse instante, a espira está totalmente imersa no campo magnético. Logo, o fluxo eletromagnético não varia. Portanto, i2 = 0.
c) Calculando a posição da espira no instante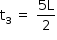 
:
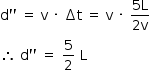
A partir do resultado obtido, conclui-se que no instante t3 a espira está parcialmente imersa no campo magnético e saindo de tal região. Assim:
- O fluxo eletromagnético diminui, logo, há campo magnético induzido na mesma direção e sentido do campo magnético original .
- Sabendo que o campo induzido é na direção z e entrando no plano xy e utilizando a regra da mão direita, conclui-se que a corrente elétrica é no sentido horário.
A intensidade da corrente induzida (i3) pode assim ser calculada:
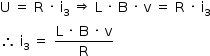
Pode-se assim representar o arranjo em t3 e as forças aplicadas na espira:
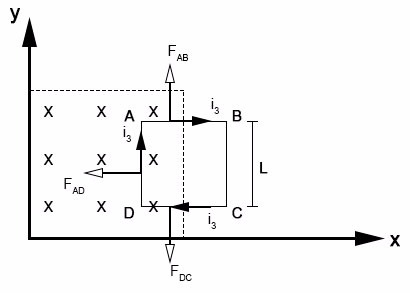
Como FAB e FDC se equilibram, a resultante das forças magnéticas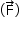 
aplicadas na espira pode assim ser calculada:
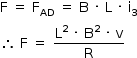
De acordo com a figura, sua direção é a do eixo x e para a esquerda.