Um alto-falante emitindo som com uma única frequência é colocado próximo à extremidade aberta de um tubo cilíndrico vertical preenchido com um líquido. Na base do tubo, há uma torneira que permite escoar lentamente o líquido, de modo que a altura da coluna de líquido varie uniformemente no tempo. Partindo-se do tubo completamente cheio com o líquido e considerando apenas a coluna de ar criada no tubo, observa-se que o primeiro máximo de intensidade do som ocorre quando a altura da coluna de líquido diminui 5 cm e que o segundo máximo ocorre um minuto após a torneira ter sido aberta.
Determine
a) o módulo da velocidade V de diminuição da altura da coluna de líquido;
b) a frequência f do som emitido pelo alto-falante.
Sabendo que uma parcela da onda sonora pode se propagar no líquido, determine
c) o comprimento de onda λ deste som no líquido;
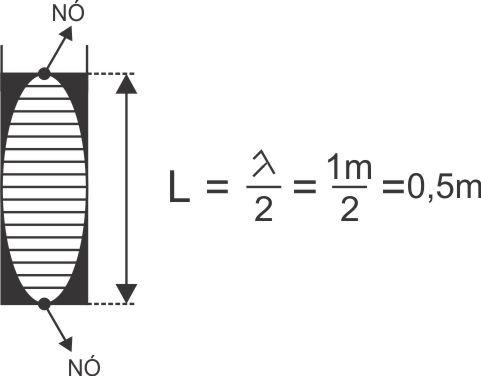
d) o menor comprimento L da coluna de líquido para que haja uma ressonância deste som no líquido.
Note e adote:
Velocidade do som no ar: var = 340 m/s.
Velocidade do som no líquido: vliq = 1700 m/s.
Considere a interface ar-líquido sempre plana.
A ressonância em líquidos envolve a presença de nós na sua superfície
a) A partir do enunciado, pode-se elaborar os dois primeiros máximos de ressonância para a situação apresentada:
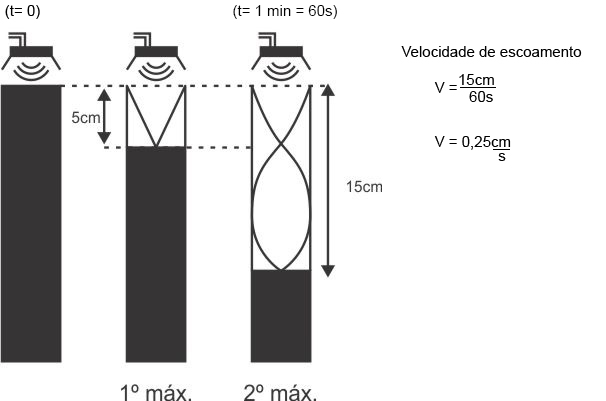
b) A partir da figura que representa o primeiro máximo de intensidade sonora:
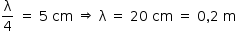
Na equação fundamental:
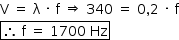
c) Ao ser refratada para o líquido, a frequência da onda permanece a mesma, ou seja, 1700 Hz.
Assim, para a onda sonora no interior do líquido:
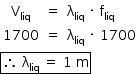
d) De acordo com o dado fornecido, o primeiro harmônico no interior do líquido obedece ao seguinte esquema: