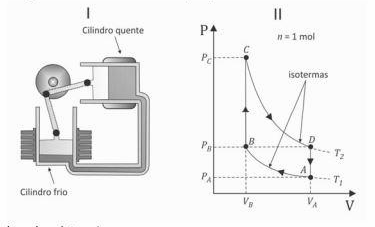
O motor Stirling, uma máquina térmica de alto rendimento, é considerado um motor ecológico, pois pode funcionar com diversas fontes energéticas. A figura I mostra esquematicamente um motor Stirling com dois cilindros. O ciclo termodinâmico de Stirling, mostrado na figura II, representa o processo em que o combustível é queimado externamente para aquecer um dos dois cilindros do motor, sendo que uma quantidade fixa de gás inerte se move entre eles, expandindo-se e contraindo-se.
Nessa figura está representado um ciclo de Stirling no diagrama P x V para um mol de gás ideal monoatômico. No estado A, a pressão é PA = 4 atm, a temperatura é = 27 °C e o volume é VA. A partir do estado A, o gás é comprimido isotermicamente até um terço do volume inicial, atingindo o estado B. Na isoterma T1, a quantidade de calor trocada é Q2 = 2.640 J, e, na isoterma T2, é Q2 = 7.910 J
Determine
a) o volume VA em litros;
b) a pressão P0, em atm, no estado D;
c) a temperatura T2.
Considerando apenas as transformações em que o gás recebe calor, determine
d) a quantidade total de calor recebido em um ciclo, QR, em J.
Note e adote:
Calor específico a volume constante: CV = 3 R/2
Constante universal do gases: R = 8 J/(mol K) = 0,08 atm ℓ / (mol K)
0 °C = 273 K
1 atm = 105 Pa
1 m3 = 1000ℓ
a) Dados:
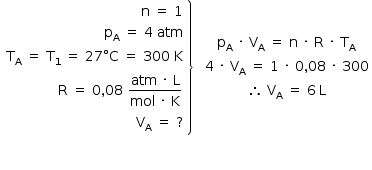
b) Note-se que pB = pD = ?
Entre os estados A e B, tem-se:
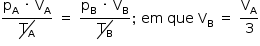
Assim:
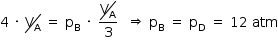
c) Entre os estados A e D: VA = VD. Assim:
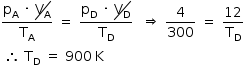
d) Na isotérmica T1, de A para B, o gás foi submetido a uma compressão (recebimento de energia mecânica) a temperatura constante. Para tal, ele deve ter cedido energia térmica (calor) ao meio. Logo, Q1 = Qcedido = 2640 J.
Na isotérmica T2, de C para D, o gás foi submetido a uma expansão (cede energia mecânica) a temperatura constante. Para tal, ele deve ter recebido energia térmica (calor) do meio. Logo, Q2 = Qrecebido = 7910 J.
Nas transformações de B para C e de D para A, as variações de temperatura, em módulo, são iguais. Como são trans formações isométricas,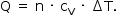 
Dessa forma: |QBC| = |QDA|. Como 
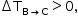nessa transformação, o gás recebeu calor:
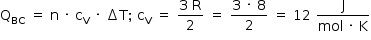
Logo: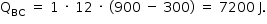 
Dessa forma, o gás RECEBE calor nas transformações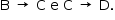 
Assim, a quantidade de calor recebido pelo gás no ciclo é:
