Um espectrônetro óptico, representado na figura, utiliza um prisma como elemento de dispersão da luz de diferentes comprimentos de onda. O espectrômetro possui uma fenda de entrada de luz, F1, uma lente convergente, L1, um prisma de vidro com ângulos internos de 60° e uma segunda lente convergente, 12, que permite a focalização do comprimento de onda da luz refratada pelo prisma em uma fenda, F2, imediatamente à frente do detector O. Cada comprimento de onda é focalizado em posições laterais diferentes no plano focal de L2.
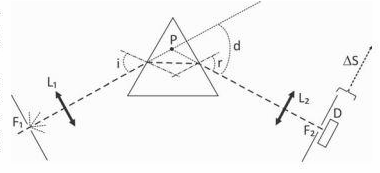
a) Determine a distância focal, F, da lente L1, posicionada a 30 mm da fenda F1, para que um feixe de luz branca, difratado pela fenda Fr, incida no prisma com os seus raios paralelos entre si.
b) O espectrômetro foi construído impondo-se que um raio de luz violeta λvioleta = 400 nm) se propague no interior do prisma (n = 1,53 para a luz violeta), paralelamente à sua face inferior. Nesta condição, determine o valor do ângulo de incidência, i, da luz branca, em relação à normal à superfície do prisma.
Para este espectrômetro, o gráfico na página de respostas apresenta o desvio angular, d, entre o feixe incidente e o feixe emergente do prisma, em função do comprimento de onda da luz refratada.
c) Determine a diferença no desvio angular, Δd, entre os feixes de luz violeta (λvioleta = 400 nm) e vermelha avermelho= 700 nm) refratados pelo prisma.
d) Considere que a distância da lente L2 ao ponto P seja 20 cm. Determine o deslocamento lateral, Δ5, em relação à posição de medida para o raio violeta, do conjunto F2 e D, para que o feixe de luz vermelha seja detectado.
Note e adote:
sen 30° = 0,50; sen 40° = 0,65; sen 50° = 0,77; sen 60° = 0,87.
Para ângulos pequenos (θ < 15°), utilizar a aproximação trigonométrica senθ ≈ tgθ ≈ θ/60 , para θ em graus.
1 nm = 10-9 m.
Índice de refração do ar: nar = 1.
A abertura de ambas as fendas é cerca de 10 vezes os comprimentos de ondas envolvidos.
a) Como a lente L1 é convergente, para que os raios provenientes da fenda F1 atinjam a lente e incidam no prisma paralelos entre si, a fenda deve estar posicionada no foco da lente. A figura a seguir ilustra essa situação:
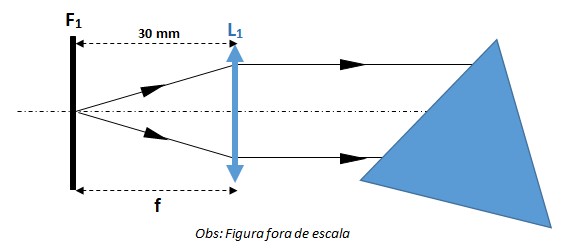
Dessa maneira, a distância focal da lente deve ser:
f = 30 mm
b) Para se determinar o ângulo de incidência i, pode-se utilizar a lei de Snell-Descartes. Para tanto, deve-se lembrar que, como o raio emerge dentro do prisma com direção paralela à base, o ângulo de refração é de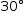 
, como ilustrado na figura a seguir.
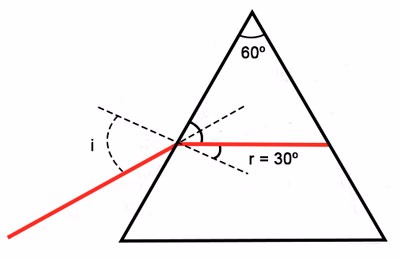
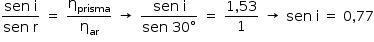
De acordo com as instruções da banca no quadro "Note e adote",
c) De acordo com o gráfico apresentado, podem-se identificar os desvios para a luz violeta 
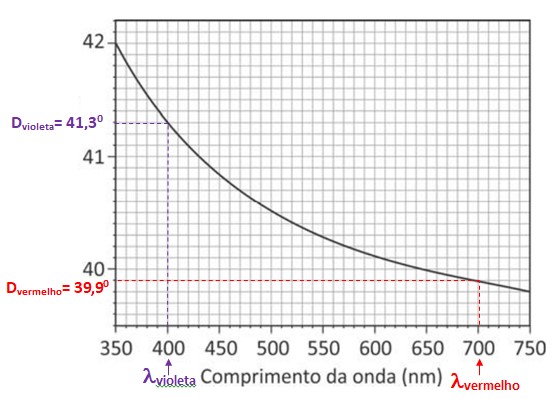
Dessa maneira, a diferença no desvio angular Δd é:
d) Inicialmente, pode-se determinar o deslocamento lateral x em relação aos raios vermelho e violeta, antes da lente L2, como ilustrado no esquema a seguir:
Como o ângulo é pequeno, podem-se fazer as considerações indicadas no "Note e adote:"
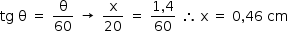
Considerando-se que a distância entre a lente L2 e o conjunto F2/D seja desprezível, é possível concluir que o deslocamento ΔS é praticamente igual a x. Dessa maneira, tem-se:
ΔS = 0,46 cm