Núcleos atômicos podem girar rapidamente e emitir raios . Nesse processo, o núcleo perde energia, passando sucessivamente por estados de energia cada vez mais baixos, até chegar ao estado fundamental, que é o estado de menor energia desse sistema. Nos laboratórios onde esses núcleos são estudados, detectores registram dados dos pulsos da radiação
emitida, obtendo informações sobre o período de rotação nuclear. A perda de energia devido à emissão de radiação eletromagnética altera o período de rotação nuclear. O gráfico mostra quatro valores do período de rotação de um dos isótopos do núcleo de érbio (158Er) durante um certo intervalo de tempo, obtidos a partir de dados experimentais.
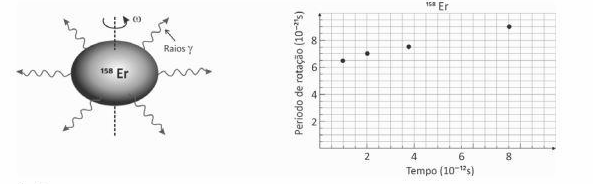
Obtenha o valor da
a) velocidade angular de rotação, ω , do núcleo no instante t = 8 x 10-12 s, em rad/s;
b) aceleração angular média, α, do núcleo entre os instantes t = 2 x 10-12 s e t = 8 x 10-12 s, em rad/s2;
c) aceleração centrípeta, αc, de uma porção de matéria nuclear localizada a uma distância R = 6 x 10-15 m do eixo de rotação nuclear para o instante t = 8 x 10-12 s;
d) energia, E, emitida pelo 158Er sob a forma de radiação eletromagnética entre os instantes t = 2 x 10-12s e t = 8 x 10-12 s.
Note e adote:
Radiação : radiação eletromagnética de frequência muito alta.
Energia rotacional do núcleo ER = (1/2) I ω2, onde I = 12 x 10-55 J s2 é constante.
π = 3
a) A partir do gráfico dado, no instante 8 · 10-12 s o período de rotação é T = 9 · 10-21 s. Utilizando a relação entre período e velocidade angular:

b) Repetindo o procedimento do item a para o instante 2 · 10-12 s:
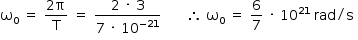
Utilizando a definição de aceleração angular média para o intervalo de tempo pedido, tem-se
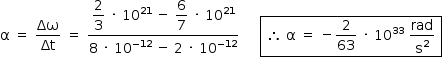
c) Admitindo o núcleo como sendo um corpo rígido, todos os seus pontos possuem a mesma velocidade angular, logo:
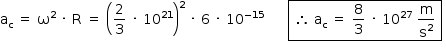
d) A energia E, emitida pelo 158Er, sob a forma de radiação eletromagnética, entre os instantes 2 · 10-12 s e 8 · 10-12 s, pode assim ser obtida:
![«math style=¨font-family:Tahoma¨ xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨14px¨»«mi mathvariant=¨normal¨»E«/mi»«mo»§#xA0;«/mo»«mo»=«/mo»«mo»§#xA0;«/mo»«mfenced open=¨|¨ close=¨|¨»«mrow»«msub»«mi mathvariant=¨normal¨»E«/mi»«mi mathvariant=¨normal¨»c«/mi»«/msub»«mo»§#xA0;«/mo»«mo»-«/mo»«mo»§#xA0;«/mo»«msub»«mi mathvariant=¨normal¨»E«/mi»«mrow»«mi mathvariant=¨normal¨»c«/mi»«mn»0«/mn»«/mrow»«/msub»«/mrow»«/mfenced»«mo»§#xA0;«/mo»«mo»=«/mo»«mo»§#xA0;«/mo»«mfenced open=¨|¨ close=¨|¨»«mrow»«mfrac»«mn»1«/mn»«mn»2«/mn»«/mfrac»«mo»§#xA0;«/mo»«mo»§#xB7;«/mo»«mo»§#xA0;«/mo»«mi mathvariant=¨normal¨»I«/mi»«mo»§#xA0;«/mo»«mo»§#xB7;«/mo»«mo»§#xA0;«/mo»«msup»«mi mathvariant=¨normal¨»§#x3C9;«/mi»«mn»2«/mn»«/msup»«mo»§#xA0;«/mo»«mo»-«/mo»«mo»§#xA0;«/mo»«mfrac»«mn»1«/mn»«mn»2«/mn»«/mfrac»«msup»«mi»I§#x3C9;«/mi»«mn»2«/mn»«/msup»«/mrow»«/mfenced»«mo»§#xA0;«/mo»«mo»=«/mo»«mo»§#xA0;«/mo»«mfenced open=¨|¨ close=¨|¨»«mrow»«mfrac»«mn»1«/mn»«mn»2«/mn»«/mfrac»«mo»§#xA0;«/mo»«mo»§#xB7;«/mo»«mo»§#xA0;«/mo»«mi mathvariant=¨normal¨»§#x399;«/mi»«mo»§#xA0;«/mo»«mo»§#xB7;«/mo»«mo»§#xA0;«/mo»«mo»(«/mo»«msup»«mi mathvariant=¨normal¨»§#x3C9;«/mi»«mn»2«/mn»«/msup»«mo»§#xA0;«/mo»«mo»-«/mo»«mo»§#xA0;«/mo»«msup»«msub»«mi mathvariant=¨normal¨»§#x3C9;«/mi»«mn»0«/mn»«/msub»«mn»2«/mn»«/msup»«mo»)«/mo»«/mrow»«/mfenced»«mo»§#xA0;«/mo»«mo»=«/mo»«mspace linebreak=¨newline¨/»«mo»§#xA0;«/mo»«mfenced open=¨|¨ close=¨|¨»«mrow»«mfrac»«mn»1«/mn»«mn»2«/mn»«/mfrac»«mo»§#xA0;«/mo»«mo»§#xB7;«/mo»«mo»§#xA0;«/mo»«mn»12«/mn»«mo»§#xA0;«/mo»«mo»§#xB7;«/mo»«msup»«mn»10«/mn»«mrow»«mo»-«/mo»«mn»55«/mn»«/mrow»«/msup»«mo»§#xA0;«/mo»«mo»§#xB7;«/mo»«mo»§#xA0;«/mo»«mfenced open=¨[¨ close=¨]¨»«mrow»«msup»«mfenced»«mrow»«mfrac»«mn»2«/mn»«mn»3«/mn»«/mfrac»«mo»§#xA0;«/mo»«mo»§#xB7;«/mo»«mo»§#xA0;«/mo»«msup»«mn»10«/mn»«mn»21«/mn»«/msup»«/mrow»«/mfenced»«mn»2«/mn»«/msup»«mo»§#xA0;«/mo»«mo»-«/mo»«mo»§#xA0;«/mo»«msup»«mfenced»«mrow»«mfrac»«mn»6«/mn»«mn»7«/mn»«/mfrac»«mo»§#xA0;«/mo»«mo»§#xB7;«/mo»«mo»§#xA0;«/mo»«msup»«mn»10«/mn»«mn»21«/mn»«/msup»«/mrow»«/mfenced»«mn»2«/mn»«/msup»«/mrow»«/mfenced»«/mrow»«/mfenced»«mspace linebreak=¨newline¨/»«mo»§#xA0;«/mo»«mo»§#xA0;«/mo»«mo»§#xA0;«/mo»«mo»§#xA0;«/mo»«mo»§#xA0;«/mo»«mo»§#xA0;«/mo»«mo»§#xA0;«/mo»«mo»§#xA0;«/mo»«mo»§#xA0;«/mo»«mo»§#xA0;«/mo»«mo»§#xA0;«/mo»«mo»§#xA0;«/mo»«mo»§#xA0;«/mo»«mo»§#xA0;«/mo»«mo»§#xA0;«/mo»«mo»§#xA0;«/mo»«mo»§#xA0;«/mo»«mo»§#xA0;«/mo»«mo»§#xA0;«/mo»«mo»§#xA0;«/mo»«mo»§#xA0;«/mo»«mo»§#xA0;«/mo»«mo»§#xA0;«/mo»«mo»§#xA0;«/mo»«mo»§#xA0;«/mo»«mo»§#xA0;«/mo»«mo»§#xA0;«/mo»«mo»§#xA0;«/mo»«mo»§#xA0;«/mo»«mo»§#xA0;«/mo»«mo»§#xA0;«/mo»«mo»§#xA0;«/mo»«mo»§#xA0;«/mo»«mo»§#xA0;«/mo»«mo»§#xA0;«/mo»«mo»§#xA0;«/mo»«mo»§#xA0;«/mo»«mo»§#xA0;«/mo»«mo»§#xA0;«/mo»«mo»§#xA0;«/mo»«mo»§#xA0;«/mo»«mo»§#xA0;«/mo»«mo»§#xA0;«/mo»«mo»§#xA0;«/mo»«mo»§#xA0;«/mo»«mo»§#xA0;«/mo»«mo»§#xA0;«/mo»«mo»§#xA0;«/mo»«mo»§#xA0;«/mo»«mo»§#xA0;«/mo»«mo»§#xA0;«/mo»«mo»§#xA0;«/mo»«mo»§#xA0;«/mo»«mo»§#xA0;«/mo»«mo»§#xA0;«/mo»«mo»§#xA0;«/mo»«mo»§#xA0;«/mo»«mo»§#xA0;«/mo»«mo»§#xA0;«/mo»«mo»§#xA0;«/mo»«mo»§#xA0;«/mo»«mo»§#xA0;«/mo»«mo»§#xA0;«/mo»«mo»§#xA0;«/mo»«mo»§#xA0;«/mo»«mo»§#xA0;«/mo»«mo»§#xA0;«/mo»«mo»§#xA0;«/mo»«mo»§#xA0;«/mo»«mo»§#xA0;«/mo»«mo»§#xA0;«/mo»«mo»§#xA0;«/mo»«mo»§#xA0;«/mo»«mo»§#xA0;«/mo»«mo»§#xA0;«/mo»«mo»§#xA0;«/mo»«mo»§#xA0;«/mo»«mo»§#xA0;«/mo»«mo»§#xA0;«/mo»«mo»§#xA0;«/mo»«mo»§#xA0;«/mo»«mo»§#xA0;«/mo»«mo»§#xA0;«/mo»«mo»§#xA0;«/mo»«mo»§#xA0;«/mo»«mo»§#xA0;«/mo»«mo»§#xA0;«/mo»«mo»§#xA0;«/mo»«mo»§#xA0;«/mo»«mo»§#xA0;«/mo»«mspace linebreak=¨newline¨/»«mo»§#xA0;«/mo»«mo»§#xA0;«/mo»«mo»§#xA0;«/mo»«mo»§#xA0;«/mo»«mo»§#xA0;«/mo»«mo»§#xA0;«/mo»«mo»§#xA0;«/mo»«mo»§#xA0;«/mo»«mo»§#xA0;«/mo»«mo»§#xA0;«/mo»«mo»§#xA0;«/mo»«mo»§#xA0;«/mo»«mo»§#xA0;«/mo»«mo»§#xA0;«/mo»«mo»§#xA0;«/mo»«mo»§#xA0;«/mo»«mo»§#xA0;«/mo»«mo»§#xA0;«/mo»«mo»§#xA0;«/mo»«mo»§#xA0;«/mo»«mo»§#xA0;«/mo»«mo»§#xA0;«/mo»«mo»§#xA0;«/mo»«mo»§#xA0;«/mo»«mo»§#xA0;«/mo»«mo»§#xA0;«/mo»«mo»§#xA0;«/mo»«mo»§#xA0;«/mo»«mo»§#xA0;«/mo»«mo»§#xA0;«/mo»«mo»§#xA0;«/mo»«mo»§#xA0;«/mo»«mo»§#xA0;«/mo»«mo»§#xA0;«/mo»«mo»§#xA0;«/mo»«mo»§#xA0;«/mo»«mo»§#xA0;«/mo»«mo»§#xA0;«/mo»«mo»§#xA0;«/mo»«mo»§#xA0;«/mo»«mo»§#xA0;«/mo»«mo»§#xA0;«/mo»«mo»§#xA0;«/mo»«mo»§#xA0;«/mo»«mo»§#xA0;«/mo»«mo»§#xA0;«/mo»«mo»§#xA0;«/mo»«mo»§#xA0;«/mo»«mo»§#xA0;«/mo»«menclose notation=¨box¨»«mo»§#xA0;«/mo»«mo»§#x2234;«/mo»«mo»§#xA0;«/mo»«mi mathvariant=¨normal¨»E«/mi»«mo»§#xA0;«/mo»«mo»=«/mo»«mo»§#xA0;«/mo»«mn»1«/mn»«mo»,«/mo»«mn»74«/mn»«mo»§#xA0;«/mo»«mo»§#xB7;«/mo»«mo»§#xA0;«/mo»«msup»«mn»10«/mn»«mrow»«mo»-«/mo»«mn»13«/mn»«/mrow»«/msup»«mo»§#xA0;«/mo»«mi mathvariant=¨normal¨»J«/mi»«mo»§#xA0;«/mo»«/menclose»«/mstyle»«/math»](https://anglo.plurall.net/sites/all/libraries/ckeditor//plugins/ckeditor_wiris/integration/showimage.php?formula=4e8ea2f7f5cbd0283ded85f9c043a36d.png)