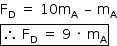Duas caixas, A e B, de massas mA e mB, respectivamente, precisam ser entregues no 40° andar de um edifício. O entregador resolve subir com as duas caixas em uma única viagem de elevador e a figura I ilustra como as caixas foram empilhadas. Um sistema constituído por motor e freios é responsável pela movimentação do elevador; as figuras II e III ilustram o comportamento da aceleração e da velocidade do elevador. O elevador é acelerado ou desacelerado durante curtos intervalos de tempo, após o que ele adquire velocidade constante.
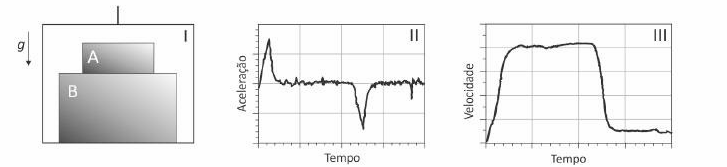
Analise a situação sob o ponto de vista de um observador parado no solo. Os itens a, b e c, referem-se ao instante de tempo em que o elevador está subindo com o valor máximo da aceleração, cujo módulo é a =1 m/s2.
a) Obtenha o módulo da força resultante, FA, que atua sobre a caixa A.
b) As figuras na página de respostas representam esquematicamente as duas caixas e o chão do elevador. Faça, nas figuras correspondentes, os diagramas de forças indicando as que agem na caixa A e na caixa B.
c) Obtenha o módulo, F5, da força de contato exercida pela caixa A sobre a caixa B.
d) Como o cliente recusou a entrega, o entregador voltou com as caixas. Considere agora um instante em que o elevador está descendo com aceleração para baixo de módulo a =1 m/s2. Obtenha o módulo, FD, da força de contato exercida pela caixa A sobre a caixa B.
Note e adote
Aceleração da gravidade : g = 10 / s2.
a) Utilizando o princípio fundamental da dinâmica:
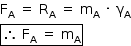
b) As forças aplicadas nos corpos A e B podem assim serem representadas:
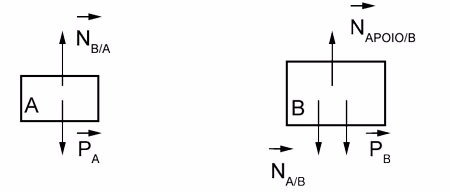
Sendo:

c) No instante analisado, o corpo está subindo e executando movimento retilíneo e acelerado, logo, podemos representar a velocidade vetorial, a aceleração vetorial e a resultante.
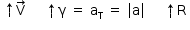
Portanto, podemos obter a resultante no corpo A:
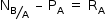
A intensidade da força de contato (Fs) exercida pela caixa A sobre a caixa B é igual à intensidade da normal que a caixa B aplica sobre a caixa A, logo:

d) No novo instante analisado, o corpo está descendo e executando movimento retilíneo e acelerado, logo, podemos representar a velocidade vetorial, a aceleração vetorial e a resultante:
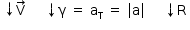
Portanto, podemos obter a resultante no corpo B:
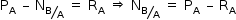
Sendo 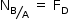 , temos:
, temos: