O prêmio Nobel de Física de 2017 foi conferido aos três cientistas que lideraram a colaboração LIGO (Laser Interferometer Gravitational -Wave Observatory), responsável pela primeira detecção direta de ondas gravitacionais, ocorrida em 14 de setembro de 2015. O LIGO é constituído por dois detectores na superfície da Terra, distantes 3.000 quilômetros entre si. Os sinais detectados eram compatíveis com os produzidos pela fusão de dois buracos negros de massas aproximadamente iguais a 36 e 29 massas solares. Essa fusão resultou em um único buraco negro de 62 massas solares a uma distância de 1,34 bilhão de anos-luz da Terra.
a) A detecção foi considerada legítima porque os sinais foram registrados com diferença de tempo compatível com a distância entre os detectores. Considerando que as ondas gravitacionais se propaguem com a velocidade da luz, obtenha a maior diferença de tempo, Δt, que pode ser aceita entre esses registros para que os sinais ainda sejam considerados coincidentes.
b) Foi estimado que, no último 0,2 s da fusão, uma quantidade de energia equivalente a três massas solares foi irradiada sob a forma de ondas gravitacionais. Calcule a potência, P, irradiada.
c) A emissão decorrente da fusão desses dois buracos negros deu origem a ondas gravitacionais, cuja potência irradiada foi maior do que a potência irradiada sob a forma de ondas eletromagnéticas por todas as estrelas do Universo. Para quantificar esta afirmação, calcule a potência total irradiada pelo Sol. Obtenha o número N de sóis necessários para igualar a potência obtida no item b.
Note e adote: Equivalência massa energia: E = mc2.
Velocidade da luz: c = 3,0 x 108 m/s.
Massa do Sol: 2,0 x 1030 kg.
Intensidade da luz irradiada pelo Sol, incidente na órbita da Terra: 1,4 kW/m2.
Distância Terra . Sol: 1,5 x 1011 m.
Área da superfície de uma esfera de raio R: 4π R2.
π = 3.
a) A distância entre os detectores é 3000 km, e a velocidade da luz é 300000 km/s. Dessa forma, o intervalo de tempo ∆t para que a onda eletromagnética percorra a distância entre os dois detectores é:
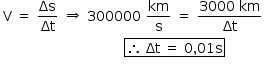
b) A quantidade de energia equivalente a três massas solares é dada por:
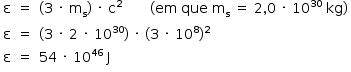
Em 0,2 s (duração do evento), a potência irradiada é:

c) A área irradiada pelo Sol na superfície que contém a Terra é:

Como a intensidade da luz irradiada pelo Sol, incidente na órbita da Terra, é 1,4 kW/m2, tem-se:

Como a potência irradiada pela fusão equivalente a 3 massas solares foi de 27 · 1047 W, o número N de sóis necessários para igualar essa potência é:
