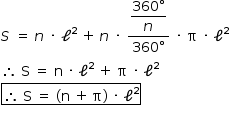Uma cerca tem formato de um polígono regular de n lados, cada lado com comprimento l. A égua Estrela pasta amarrada à cerca por uma corda, também de comprimento l, no exterior da região delimitada pelo polígono. Calcule a área disponível para pasto supondo que:
a) a extremidade da corda presa à cerca está fixada num dos vértices do polígono;
b) a extremidade da corda pudesse deslizar livremente ao longo de todo o perímetro da cerca.
a) Considere a figura a seguir, que contém uma parte do polígono regular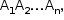 
bem como a área disponível para pasto, hachurada:
Sendo ê a medida de um ângulo externo do polígono, tem-se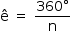 
e, assim, a área S pedida é dada pela área de um setor circular cujo raio mede l e o ângulo central 
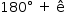, ou seja:
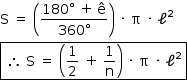
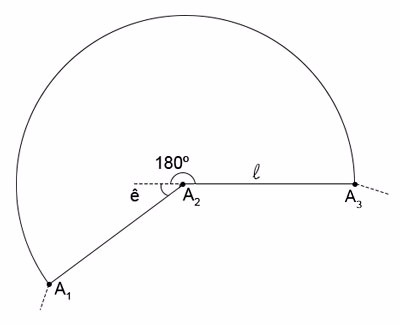
b) Considere a figura a seguir, que contém uma parte do polígono A1A2A3...An:
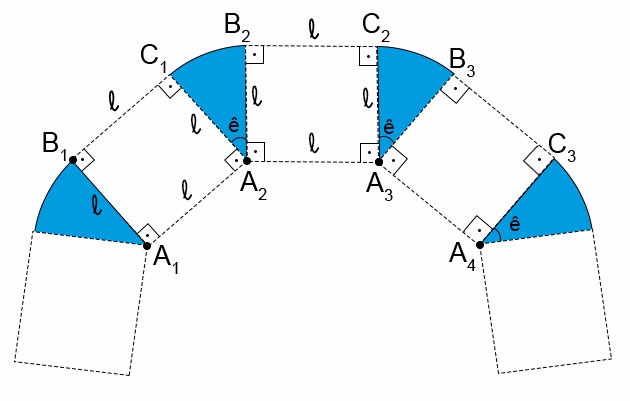
No caso em que a extremidade da corda desliza sobre todo o perímetro do polígono, a área disponível para pasto é dada pela soma das áreas de n quadrados, todos com lados de medida ℓ e as áreas de n setores circulares congruentes, com raios de medida ℓ e ângulo central 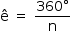, ou seja, a área S pedida é dada por:
