No plano cartesiano real, considere o triângulo ABC, em que A = (5,0), B = (8,0), C = (5,5), e a reta de equação y = αx, 0 < α < 1. Seja ƒ(α) a área do trapézio ABED, em que D é a intersecção da reta y = αx com a reta de equação x = 5, e o segmento DE é paralelo ao eixo Ox.
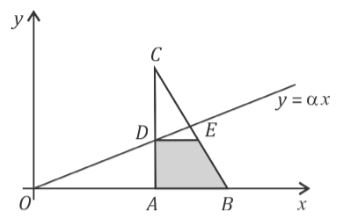
a) Encontre o comprimento do segmento DE em função de α.
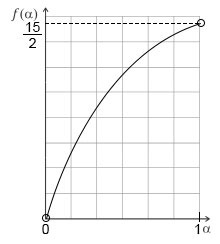
b) Expresse ƒ(α) e esboce o gráfico da função ƒ.
a) Do enunciado, tem-se a seguinte figura:
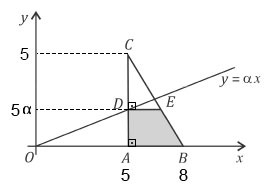
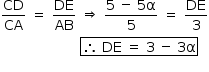
Da figura, tem-se BA = 3, CA = 5 e CD = 5 - 5α.
Como os triângulos CDE e CAB são semelhantes, tem-se:
b) A área S do trapézio ABED é dada por:
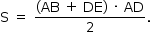
Assim, 
O gráfico de f(α), com 0 < α < 1, é dado por: