O gráfico representa uma hipérbole, dada pela função real . Sabe-se que ABCD é um retângulo,
que é diagonal do retângulo EBCF e que a área da região indicada em rosa é igual a 4,7 cm2.
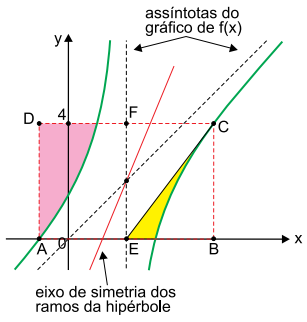
a) Determine as coordenadas (x, y) do ponto A.
b) Calcule a área da região indicada em amarelo no gráfico.
a) Sendo A o ponto de intersecção do gráfico de f(x) com o eixo das abscissas, tem-se que f(x) = 0
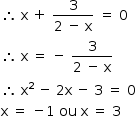
Como A possui abscissa negativa, tem-se que x = –1.
Portanto, A possui coordenadas (–1, 0)
Resposta: A = (–1, 0).
b) Considere a figura abaixo:
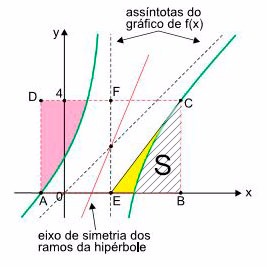
A área da região indicada em amarelo será a diferença entre a área do triângulo BCE e a área S indicada no gráfico acima.
Como os ramos da hipérbole são simétricos, tem-se que a área S indicada no gráfico acima é igual à área indicada em rosa, ou seja, S = 4,7 cm2.
Tem-se, da figura, que o ponto C possui ordenada y = 4.
Sendo f(x) = 4, tem-se:
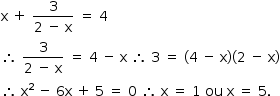
Portanto, da figura, tem-se que C(5, 4)
A abscissa dos pontos B e C são iguais.
Como AO = 1, OB = 5 e AE = EB, então OE = 2 e EB = 3.
A área do triângulo BCE será dada por: 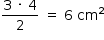
Portanto, a área indicada em amarelo será 6 – 4,7 = 1,3 cm2.
Resposta: 1,3 cm2.