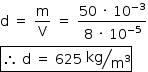Uma esfera de massa 50 g está totalmente submersa na água contida em um tanque e presa ao fundo por um fio, como mostra a figura 1. Em dado instante, o fio se rompe e a esfera move-se, a partir do repouso, para a superfície da água, onde chega 0,60 s após o rompimento do fio, como mostra a figura 2.
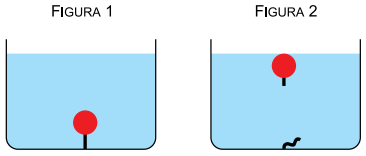
a) Considerando que, enquanto a esfera está se movendo no interior da água, a força resultante sobre ela é constante, tem intensidade 0,30 N, direção vertical e sentido para cima, calcule, em m/s, a velocidade com que a esfera chega à superfície da água.
b) Considerando que apenas as forças peso e empuxo atuam sobre a esfera quando submersa, que a aceleração gravitacional seja 10 m/s2 e que a massa específica da água seja 1,0 × 103 kg/m3, calcule a densidade da esfera, em kg/m3.
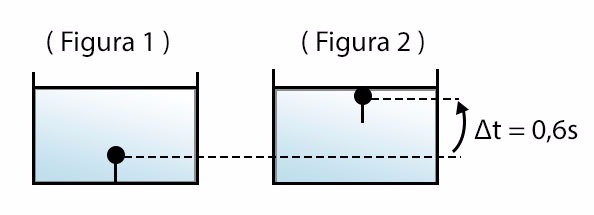
a) As figuras a seguir representam, de forma esquemática, o instante em que o fio se rompe (Figura 1) e aquele no qual a esfera atinge a superfície da água (Figura 2):
Utilizando o princípio fundamental da dinâmica:
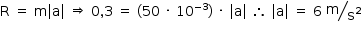
De acordo com o enunciado, a resultante é constante, logo, o movimento é uniformemente variado.
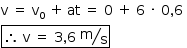
b) A figura a seguir representa as forças aplicadas na esfera, a resultante e a aceleração que lhe são associadas em qualquer instante durante a subida.
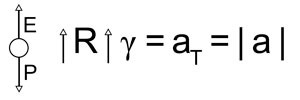
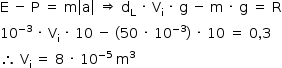
Utilizando a definição de densidade: