Uma chapa retangular metálica, de área igual a 8,132 m², passa por uma máquina que a transforma, sem nenhuma perda de material, em uma telha ondulada. A figura mostra a telha em perspectiva.

A curva que liga os pontos A e B, na borda da telha, é uma senoide.
Considerando um sistema de coordenadas ortogonais com origem em A, e de forma que as coordenadas de B, em centímetros, sejam (195, 0), a senoide apresentará a seguinte configuração:

a) Calcule o comprimento da senoide indicada no gráfico, do ponto A até o ponto B.
b) Determine a expressão da função cujo gráfico no sistema de coordenadas é a senoide de A até B. Determine o domínio, a imagem e o período dessa função.
Seja x o comprimento da senoide, do ponto A ao ponto B.
Do enunciado, a área da chapa retangular é igual 8,132 m2.

b) Do enunciado, tem-se a figura:
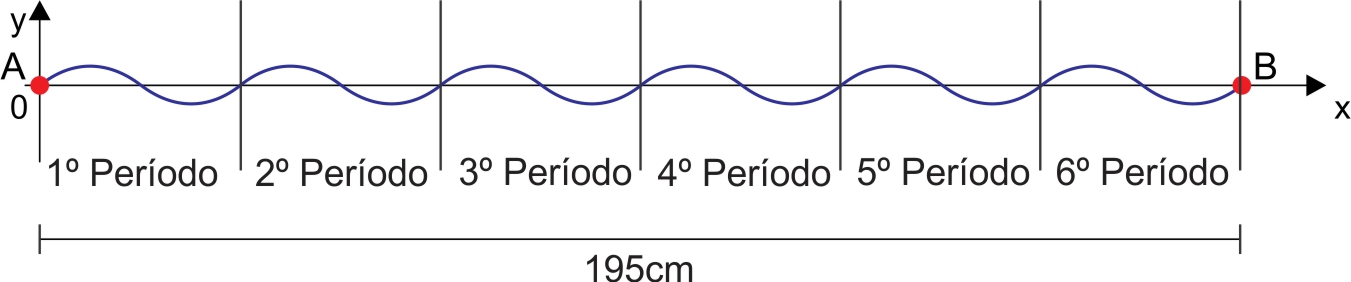
Dela, tem-se que a frequência é igual a 6.
Portanto, o período será dado por 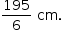
A expressão cujo gráfico é a senoide é dada por 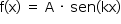 .
.
Assim,
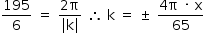
Como a amplitude é 4 cm, então A = 2
Logo, 
![«math style=¨font-family:Tahoma¨ xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨14px¨»«mi»Resp«/mi»«mo».«/mo»«mo»:«/mo»«mspace linebreak=¨newline¨/»«mi»Dom§#xED;nio«/mi»«mo»:«/mo»«mo»§#xA0;«/mo»«mo»[«/mo»«mn»0«/mn»«mo»,«/mo»«mo»§#xA0;«/mo»«mn»195«/mn»«mo»]«/mo»«mspace linebreak=¨newline¨/»«mi»Imagem«/mi»«mo»:«/mo»«mo»§#xA0;«/mo»«mo»[«/mo»«mo»-«/mo»«mn»2«/mn»«mo»,«/mo»«mo»§#xA0;«/mo»«mn»2«/mn»«mo»]«/mo»«mspace linebreak=¨newline¨/»«mi»Per§#xED;odo«/mi»«mo»:«/mo»«mo»§#xA0;«/mo»«mfrac»«mn»195«/mn»«mn»6«/mn»«/mfrac»«mo»§#xA0;«/mo»«mi»cm«/mi»«mspace linebreak=¨newline¨/»«mi»Express§#xE3;o«/mi»«mo»:«/mo»«mo»§#xA0;«/mo»«mi mathvariant=¨normal¨»f«/mi»«mn»1«/mn»«mo»(«/mo»«mi mathvariant=¨normal¨»x«/mi»«mo»)«/mo»«mo»§#xA0;«/mo»«mo»=«/mo»«mo»§#xA0;«/mo»«mo»+«/mo»«mn»2«/mn»«mo»§#xA0;«/mo»«mo»§#xB7;«/mo»«mo»§#xA0;«/mo»«mi»sen«/mi»«mfenced»«mfrac»«mrow»«mo»+«/mo»«mn»4«/mn»«mi»§#x3C0;x«/mi»«/mrow»«mn»65«/mn»«/mfrac»«/mfenced»«mo»§#xA0;«/mo»«mo»§#xA0;«/mo»«mo»§#xA0;«/mo»«mi»ou«/mi»«mo»§#xA0;«/mo»«mi»ainda«/mi»«mo»,«/mo»«mo»§#xA0;«/mo»«mo»§#xA0;«/mo»«mi mathvariant=¨normal¨»f«/mi»«mn»2«/mn»«mo»(«/mo»«mi mathvariant=¨normal¨»x«/mi»«mo»)«/mo»«mo»§#xA0;«/mo»«mo»=«/mo»«mo»§#xA0;«/mo»«mo»-«/mo»«mn»2«/mn»«mo»§#xA0;«/mo»«mo»§#xB7;«/mo»«mo»§#xA0;«/mo»«mi»sen«/mi»«mfenced»«mfrac»«mrow»«mo»-«/mo»«mn»4«/mn»«mi»§#x3C0;x«/mi»«/mrow»«mn»65«/mn»«/mfrac»«/mfenced»«/mstyle»«/math»](https://anglo.plurall.net/sites/all/libraries/ckeditor//plugins/ckeditor_wiris/integration/showimage.php?formula=1f56ac4dc8e2d6c26268d4d00cf58c01.png)