Em um tapete retangular decorado com círculos idênticos, o círculo de centro C tangencia as laterais do tapete em P e Q. O ponto R pertence à circunferência desse círculo e está à distância de 18 cm e de 25 cm das laterais do tapete, como mostra a figura.

a) Calcule a distância de R até o canto superior do tapete, indicado por S. Deixe a resposta indicada com raiz quadrada.
b) Calcule o raio dos círculos que compõem a decoração do tapete.
Da figura do enunciado, tem-se:
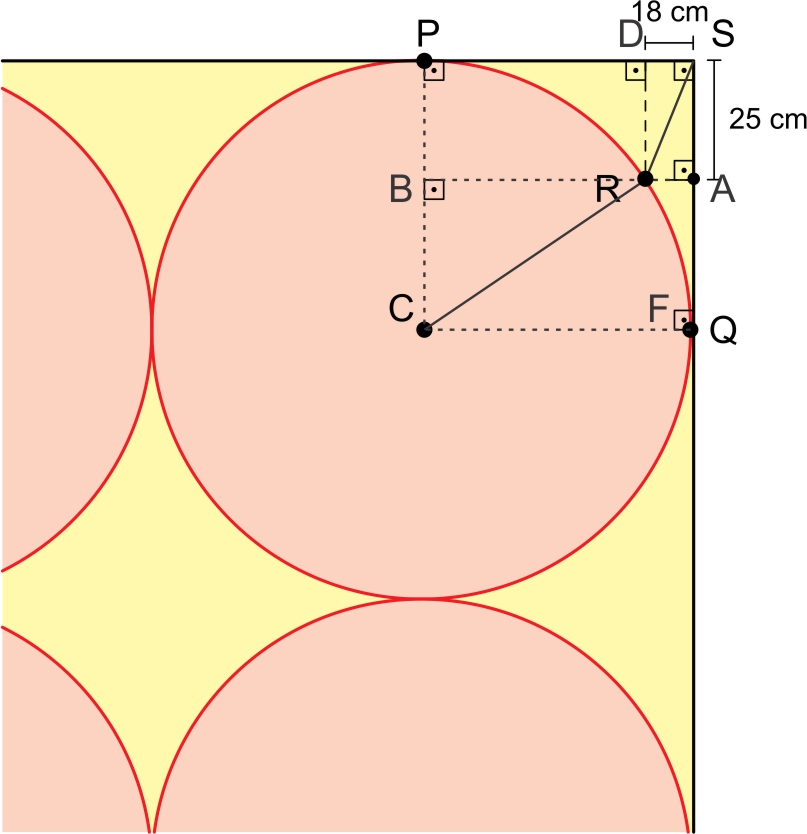
BP = SA = 25 cm
