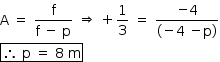Em um parque de diversões existem dois grandes espelhos dispostos verticalmente, um de frente para o outro, a 10 m de distância um do outro. Um deles é plano, o outro é esférico convexo. Uma criança se posiciona, em repouso, a 4 m do espelho esférico e vê as duas primeiras imagens que esses espelhos formam dela: IP, formada pelo espelho plano, e IC, formada pelo espelho esférico, conforme representado na figura.
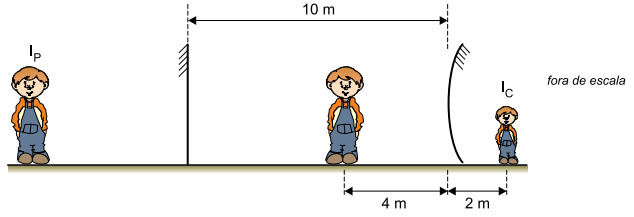
Calcule:
a) a distância, em metros, entre IP e IC.
b) a que distância do espelho esférico, em metros, a criança deveria se posicionar para que sua imagem IC tivesse um terço de sua altura.
a) Para objetos reais, o espelho plano forma imagens virtuais e simétricas em relação ao plano do espelho, como ilustrado a seguir:
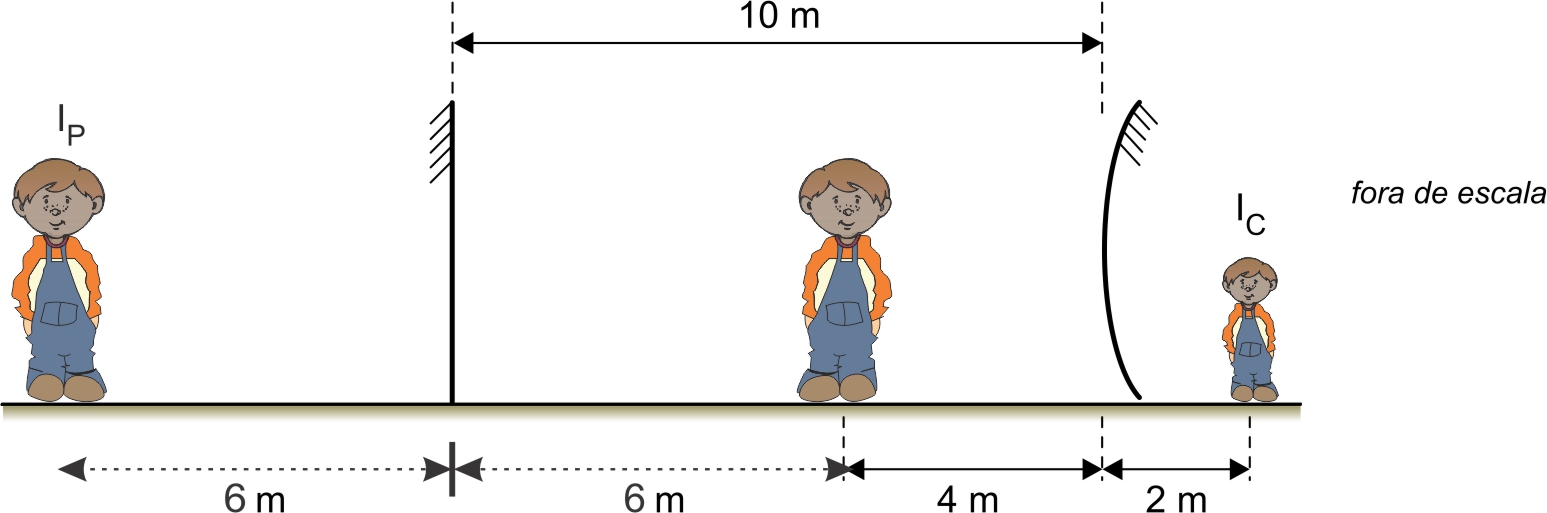
De acordo com a figura acima, pode-se determinar a distância entre Ip e Ic:
D = 6 + 10 + 2
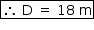
b) Com os dados apresentados para o espelho esférico, pode-se determinar sua abscissa focal:
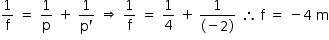
De acordo com a equação do aumento linear, tem-se: