Para a preparação de um café, 1 L de água é aquecido de 25 ºC até 85 ºC em uma panela sobre a chama de um fogão que fornece calor a uma taxa constante. O gráfico representa a temperatura (θ) da água em função do tempo, considerando que todo o calor fornecido pela chama tenha sido absorvido pela água.
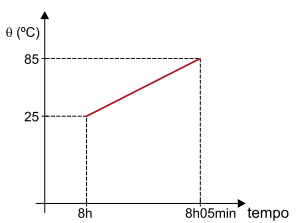
Após um certo período de tempo, foram misturados 200 mL de leite a 20 ºC a 100 mL do café preparado, agora a 80 ºC, em uma caneca de porcelana de capacidade térmica 100 cal/ºC, inicialmente a 20 ºC. Considerando os calores específicos da água, do café e do leite iguais a 1 cal/(g ·ºC), as densidades da água, do café e do leite iguais a 1 kg/L, que 1 cal/s = 4 W e desprezando todas as perdas de calor para o ambiente, calcule:
a) a potência, em W, da chama utilizada para aquecer a água para fazer o café.
b) a temperatura, em ºC, em que o café com leite foi ingerido, supondo que o consumidor tenha aguardado que a caneca e seu conteúdo entrassem em equilíbrio térmico.
a) De acordo com o gráfico apresentado, pode-se calcular a potência (em cal/s) por meio da definição de potência média:
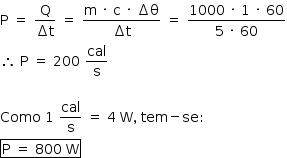
b) Considerando-se o sistema termicamente isolado, tem-se: