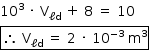Dois corpos, A e B, de massas 10 kg e 8 kg, respectivamente, cinco polias e dois fios constituem um sistema em equilíbrio, como representado na figura. O corpo A está parcialmente mergulhado na água, com 40 cm de sua altura imersos e com sua base inferior paralela ao fundo do recipiente e ao nível da água.
Adotando g = 10 m/s2, densidade da água igual a 103 kg/m3 e considerando que os fios e as polias sejam ideais e que o teto seja paralelo ao solo horizontal, calcule:
a) a diferença entre as pressões, em Pa, às quais estão submetidas as bases superior e inferior do corpo A.
b) o volume do corpo A, em m3, que se encontra abaixo da superfície da água.
a) A pressão atmosférica atua tanto na face superior quanto na face inferior do corpo A. Logo, a diferença de pressão entre essas duas faces corresponde, apenas, à pressão hidrostática.
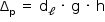
Sendo dℓ = 103 kg/m3, g = 10 m/s2, e h = 0,4 m, tem-se:
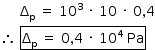
b) 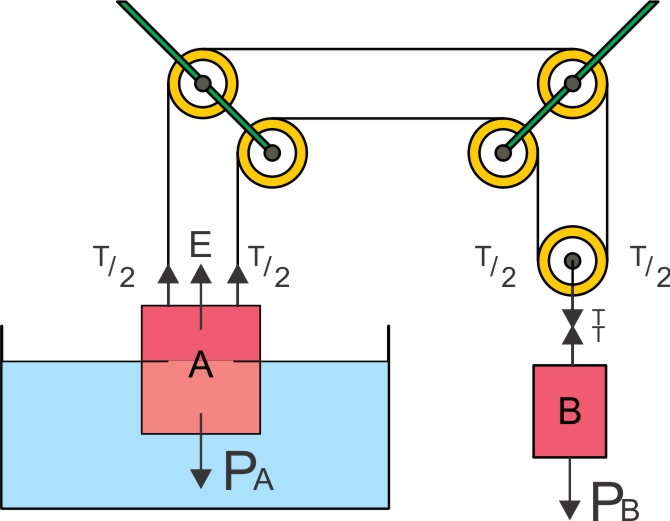
Os corpos A e B estão em equilíbrio, logo:
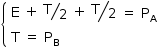
Portanto, E + PB = PA
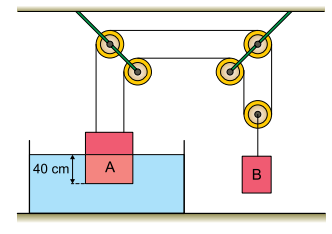
Sendo E = dℓ · Vℓd · g, PA = MA · g e PB = MB · g, tem-se:
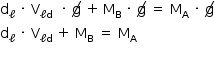
Substituindo dℓ = 103 kg/m3, MB = 8 kg e MA = 10 kg na expressão anterior, tem-se: