Um avião bombardeiro sobrevoa uma superfície plana e horizontal, mantendo constantes uma altitude de 500 m e uma velocidade de 100 m/s. Fixo no solo, um canhão antiaéreo será disparado com a intenção de acertar o avião. Considere que o avião e o canhão estejam contidos em um mesmo plano vertical, despreze a resistência do ar e adote g = 10 m/s2.
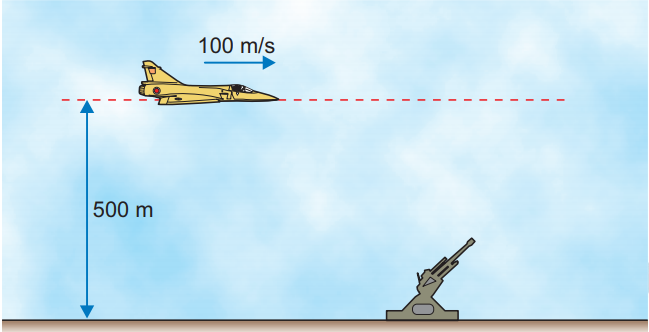
a) Quantos metros antes da vertical que passa pelo canhão o piloto do avião deve abandonar uma bomba para acertá-lo no solo?
b) Considere que o canhão não tenha sido atingido pela bomba e que, na tentativa de acertar o avião, um artilheiro dispare desse canhão um projétil com velocidade inicial v0, exatamente no momento em que o avião passa verticalmente sobre ele. Desprezando as dimensões do avião e considerando que o avião não altere sua velocidade, qual o mínimo valor de v0 para que o artilheiro tenha sucesso?
a) Representando, na figura a seguir, a situação descrita no enunciado e associando os eixos "x" e "y" pertinentes ao estado proposto:
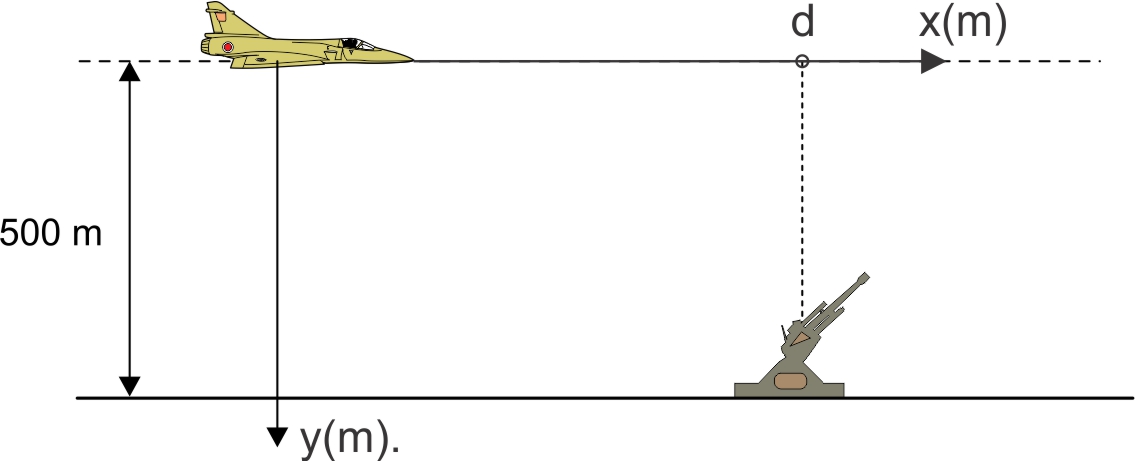
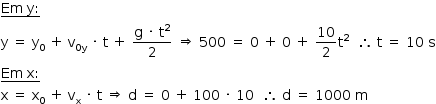
b) Para que v0 seja mínima:
- Em x: A mínima componente da velocidade na direção x deve ser 100 m/s. Para valores menores que esse, o avião, na direção x, distancia-se da bomba, não havendo encontro.
- Em y: A mínima componente da velocidade y deve ser 100 m/s, que é o menor valor de v0y para que a bomba atinja a altura de 500 m. Portanto pode-se assim representar a velocidade vetorial
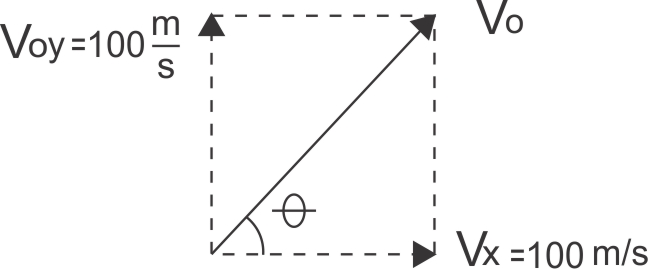
Utilizando o teorema de Pitágoras: