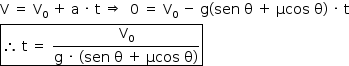Um bloco é lançado com velocidade inicial vo, em movimento ascendente, num longo plano inclinado que forma um ângulo θ com a direção horizontal. O coeficiente de atrito cinético entre as superfícies do bloco e do plano vale μ e o módulo da aceleração da gravidade local vale g. A expressão algébrica que possibilita determinar a máxima distância percorrida pelo bloco durante a subida e o respectivo tempo gasto nesse deslocamento é:
Representando as forças, as componentes e as medidas pertinentes à análise pedida:
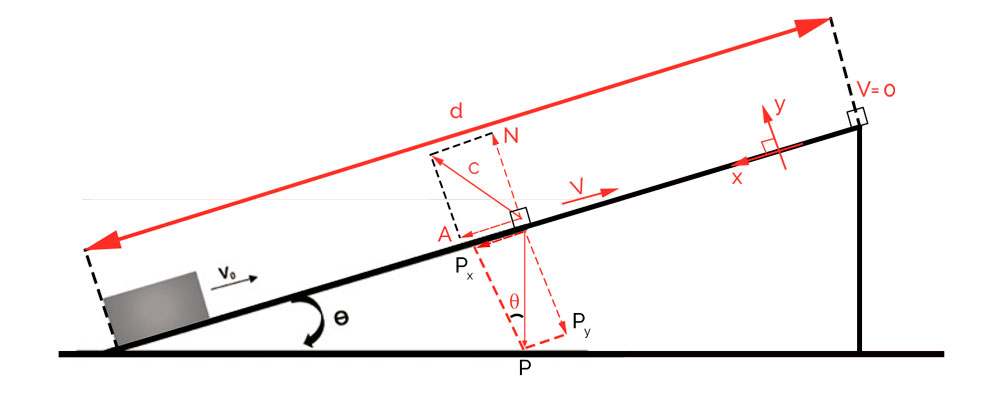
A partir do triângulo formado pelo peso e suas componentes:
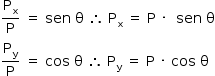
Na direção y:
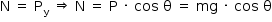
Na direção x:

De acordo com a expressão anterior, pode-se concluir que a aceleração escalar é constante. Logo, o movimento é uniformemente variado:
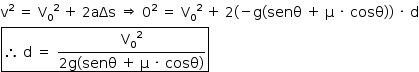
Usando a função horária da velocidade para esse movimento: