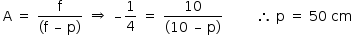Um objeto real de 10cm de altura é posicionado a 30cm do centro óptico de uma lente biconvexa, perpendicularmente ao seu eixo principal. A imagem conjugada tem 2,5cm de altura. Para produzirmos uma imagem desse mesmo objeto e com as mesmas características, utilizando, porém, um espelho esférico, cujo raio de curvatura é igual a 20cm, a que distância do vértice, em cm, da superfície refletora do espelho ele deverá ser posicionado, perpendicularmente ao seu eixo principal?
De acordo com o enunciado, a imagem formada pela lente biconvexa (convergente) é menor que o objeto. Dessa maneira, pode-se concluir que ela é invertida e, portanto, é possível calcular o aumento (A):
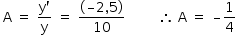
O espelho esférico capaz de obter uma imagem com as mesmas características é o espelho côncavo, cuja abscissa focal é 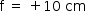 .
.
Sendo assim, de acordo com a equação do aumento, tem-se: