Uma circunferência tangencia o lado BC de um triângulo ABC no ponto F e intersecta os lados AB e AC desse triângulo, nos pontos E e D respectivamente, conforme mostra a figura.
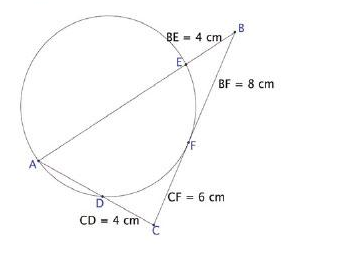
Sabendo que essa circunferência passa pelo ponto A, a distância entre os pontos D e E, em cm, é igual a
Da potência de um ponto em relação à circunferência tem-se que:

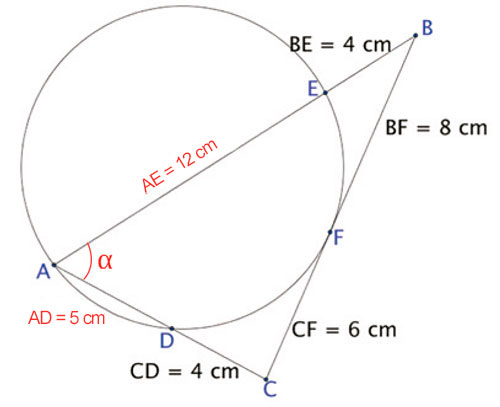
Sendo α a medida do ângulo CÂB, tem-se:
- No triângulo ABC
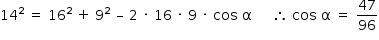
- No triângulo ADE