O polinômio p(x) = 6x4 + x3 - 63x2 + 104x - 48 possui 4 raízes reais, sendo que -4 é a única raiz negativa. Sabendo que o produto de duas das raízes desse polinômio é -4, a diferença entre as duas maiores raízes é
- a
- b
- c
- d
Como a soma dos coeficientes de p(x) é 0, o número 1 é uma de suas raízes. Aplicando o algoritmo de Briot-Ruffini, tem-se:
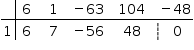
Como –4 é outra raiz de p(x), –4 também é raiz do quociente 6x3 + 7x2 – 56x + 48. Aplicando o algoritmo novamente, chega-se a:
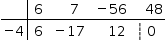
Assim, as raízes restantes são as da equação: 6x2 – 17x + 12 = 0.
Resolvendo, chega-se a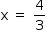 
ou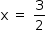 
. Como essas são as maiores raízes, a diferença entre elas (em módulo) é igual a 
.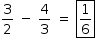