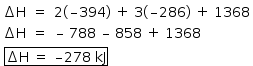Observe a equação de formação de etanol a seguir:
2 Cgraf + 3 H2(g) + ½ O2(g) → C2H6O(l)
Com base nas equações abaixo que resultam na reação de interesse, calcule o ∆H da reação de formação do etanol.
I. Cgraf + O2(g) → CO2(g) ∆H = -394 kJ/mol
II. H2(g) + ½ O2(g) → H2O(l) ∆H = -286 kJ/mol
III. C2H6O(l) + 3 O2(g) → 2 CO2(g) + 3 H2O(l) ∆H = -1368 kJ/mol
Aplicando a Lei de Hess:
- Equação I: multiplicar por 2
- Equação II: multiplicar por 3
- Equação III: inverter a equação
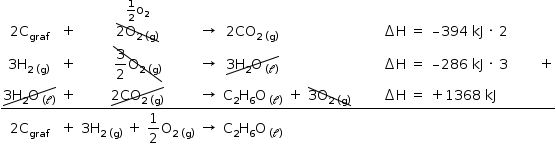
Somando os ΔH: